第四章:字符串,数组,广义表(数据结构)
串即字符串,是由零个或多个字符组成的有限序列,是数据元素为单个字符的特殊线性表。
为何要单独讨论“串”类型?
1) 字符串操作比其他数据类型更复杂(如拷贝、连接操作)
2) 程序设计中,处理对象很多都是串类型
| 如下陈述中正确的是 () 。 |
| A.串是一种特殊的线性表 |
| B.串的长度必须大于零 |
| C.串中元素只能是字母 |
| D.空串就是空白串 |
| A |
|
正确答案 答案解析 |
| 设有两个串p和q,求q在p中首次出现位置的运算称作( )。 |
| A.连接 |
| B.模式匹配 |
| C.求子串 |
| D.求串长 |
| B |
|
正确答案 答案解析 |
类型特点:
1 )只有引用型操作,没有加工型操作;
2 )数组是多维的结构,而存储空间是一个一维的结构。
有两种顺序映象的方式:
1 )以行序为主序(低下标优先);
2 )以列序为主序(高下标优先);
以常规方法,即以二维数组表示
高阶的稀疏矩阵时产生的问题:
( 1 )零值元素占了很大空间;
( 2 )计算中进行了很多和零值的运算,遇除法,还需判别除数是否为零;
因为
①数组特点:结构固定—一维数和维界不变。
②数组基本操作:初始化、销毁、取元素、修改元素值。
—般不做插入和删除操作。
所以:—般都是采用顺序存储结构来表示数组。
注意:数组可以是多维的,但存储数据元素的内存单元地址是一维的,因
此,在存储数组结构之前,需要解决将多维关系映射到一维关系的问题。
|
74.数据结构王道最后8套题第七套第一,2题050页
2.设有一个 10 阶对称矩阵 A,采用压缩存储方式,以行序为主存储,a1,1为第一个元素,其存储地址为 1,每个元素占一个地址空间,则 a8,5的地址可能是( )。 |
| A.13 |
| B.33 |
| C.18 |
| D.40 |
| B |
| 2.B。 【解析】考查特殊矩阵的存储。对称矩阵可以存储其下三角,也可以存储其上三角。数组下标从 1 开始,当存储下三角元素时,在 a8,5的前面有 7 行,第 1 行有 1 个元素,第 2 行有 2 个元素,…,第 7 行有 7 个元素,这 7 行共有(1+7)×7/2=28 个元素,在第 8 行中,a8,5的前面有 4 个元素,所以,a8,5前面有 28+4=32 个元素,其地址为 33。当存储上三角元素时,a8,5对应于 a5,8,地址为 38,无此选项,故只可能选B。 |
在一个 n 阶方阵 A 中,若元素满足下述性质:
a_ij=a_ji ,0≤i, j≤n-1则称 A 为对称矩阵。
对称矩阵中的元素关于主对角线对称,故只要存储矩阵中上三角或下三角中的元素,让每两个对称的元素共享一个存储空间,这样,能节约近一半的存储空间。不失一般性,按 " 行优先顶序 " 存储主对角线(包括对角线)以下的元素,其存储形式如图所
对称矩阵若对一个n阶方阵A[1.n][1...n]中的任意元素ai,j;都有ai,j= a(1<I,j≤n),则称其为对称矩阵。
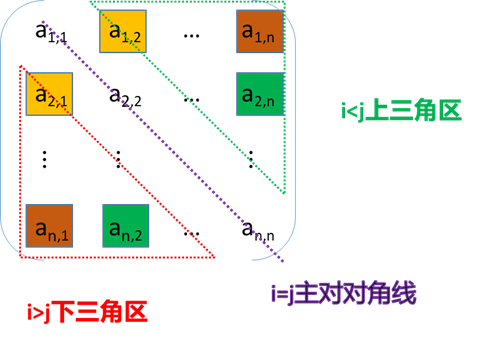
存放数组B[n(n+1)/2]
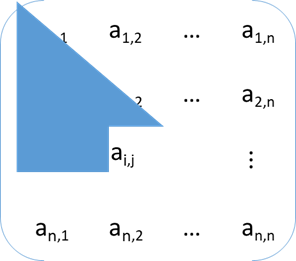 |
|
对称矩阵上下三角中的元素数均为:
三角矩阵 若对一个n阶方阵A[1..n][1...n]中上(下)三角区元素均为同一常量,则称为下(上)三角矩阵。
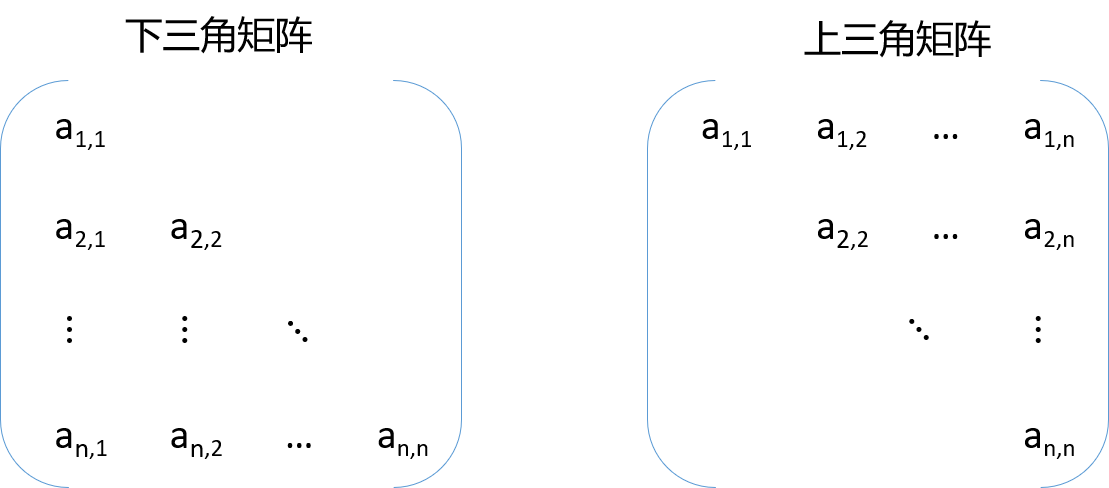
下三角矩阵中,上三角区的所有元素均为同一常量。其存储思想与对称矩阵类似,不同之处在于存储完下三角区和主对角线上的元素之后,紧接着存储对角线上方的常量一次,故可以将下三角矩阵A[1…n][1…n]压缩存储在B[n(n+1)/2+1]中元素下标之间的对应关系为
| \(数组下标k=\begin{equation} \begin{cases}\frac {i(i-1)}{2}+j-1 &\ i \ge j, \\ \frac{n(n-1)}{2} & i<j . \\ \end{cases} \end{equation} \) |
下三角矩阵的在内存中的压缩存储形式如图所示

上三角矩阵中,下三角区的所有元素均为同一常量。只需存储主对角线、上三角区上的元素和下三角区的常量一次,可以将其压缩存储在B[n(n+1)2+1]中
在数组B中,位于元素ai,j(i≤j)前面的元素个数
第1行:n个元素
第2行:n-1个元素
第i-1行:n-i+2个元素
第ⅰ行:j-i个元素
故,元素ai,j在数组B中的下标K=n+(n-1)+…+(n-i+2)+(-i+1)-1=\(\frac{(i-1)(2n-i+2)}{2}+(j-i)\).因此,元素下标之间的对应关系如下:
| \(数组下标k=\begin{equation} \begin{cases}\frac {(i-1)(2n-i+2)}{2}+j-i & i \le j, \\ \frac{n(n+1)}{2} & i>j . \\ \end{cases} \end{equation} \) |
上三角矩阵的在内存中的压缩存储形式如图所示

三对角矩阵 若对一个n阶方阵A中的任意元素ai,j,当|i-j|>1,有ai,j=0(1<I,j≤n),则称为三对角矩阵。
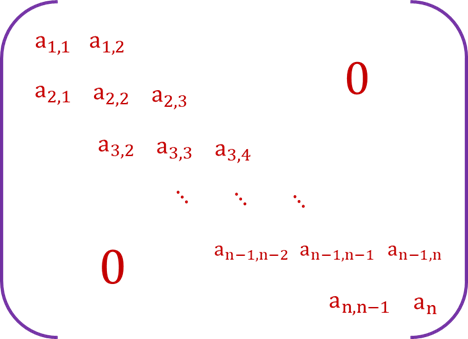
数组下标k = 3*(i-1)-1+j-i+1+1-1
= 2i+j-3
若k已知,求i,j?
i = ⌊(k+1)/3+1⌋
j= k-2i+3
|
1.数据结构2018年真题,第一,3题 3. 设有一个 12×12 的对称矩阵 M ,将其上三角部分的元素 mi, j(1≤ i ≤ j ≤12)按行优先存人 C语言的一维数组 N 中,元素 m6, 6 在 N 中的下标是 。 |
| A . 50 |
| B. 51 |
| C. 55 |
| D. 66 |
| A |
|
答案:A
|
例:设有一个二维数组A[m][n]按行优先顺序存储,假设A[0][0]存
放位置在644(10),A[2][2]存放位置在676(10),每个元素占一个空间,
问A[3][3](10)存放在什么位置?(脚注(10),表示用10进制表示。)
设数组元素A[i][j]存放在起始地址为Loc ( i,j)的存储单元中
Loc ( 2,2)= Loc ( 0,0 )+2* n +2 = 644 +2*n+2 = 676.
n = ( 676-2-644)/2 = 15
Loc ( 3,3 )= Loc ( 0,0)+(3* 15+ 3)*1= 644+45+ 3 = 692.
已知二维数组Am,m采用按行优先顺序存放,每个元素占K个存储单元,并且第一个元素的存储地址为Loc(a11),请写出求Loc(aij)的计算公式。如果采用列优先顺序存放呢?(10分)
解:公式教材已给出,此处虽是方阵,但行列公式仍不相同
按行存储的元素地址公式是:Loc(aij)=Loc(a11)+[(i-1)*n+(j-1)]*k
按列存储的元素地址公式是:Loc(aij)=Loc(a11)+[(j-1)*m+(i-1)]*k
8.设数组a[1…60,1…70]的基地址为2048,每个元素占2个存储单元,若以列序为主序顺序存储,则元素a[32,58]的存储地址为____
答:不考虑0行0列,利用列优先公式:Loc(aij)=Loc(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c)]*L
得:LOC(a32,58)=2048+[(58-1)*(60-1+1)+32-1]*2=8950
已知二维数组A[M][N]采用按行为主的顺序存储结构,每个元素占k个存储单元,第一个元素的地址为LOC(A[0][0]),那么,LOC(A[i][j])= ____________。
Loc(A[0][0])+k*(i*N+j)
稀疏矩阵:设在mx n的矩阵中有t个非零元素。
令
δ= t/(m x n)
当δ≤0.05时称为稀疏矩阵。
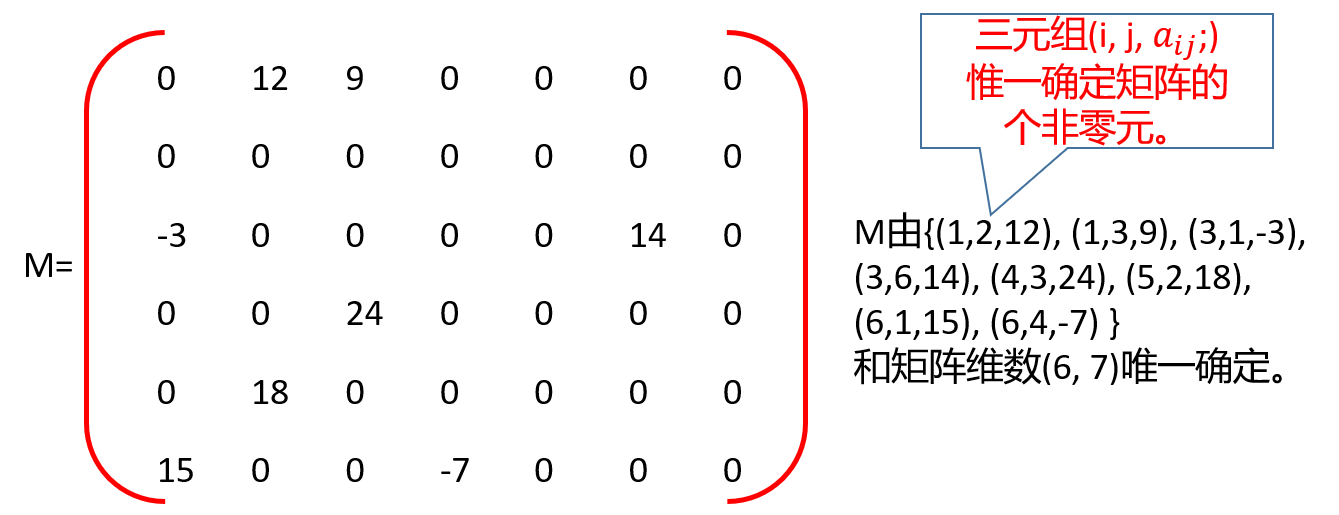
压缩存储原则:存各非零元的值、行列位置和矩阵的行列数。
三元组的不同表示方法可决定稀疏矩阵不同的压缩存储方法。
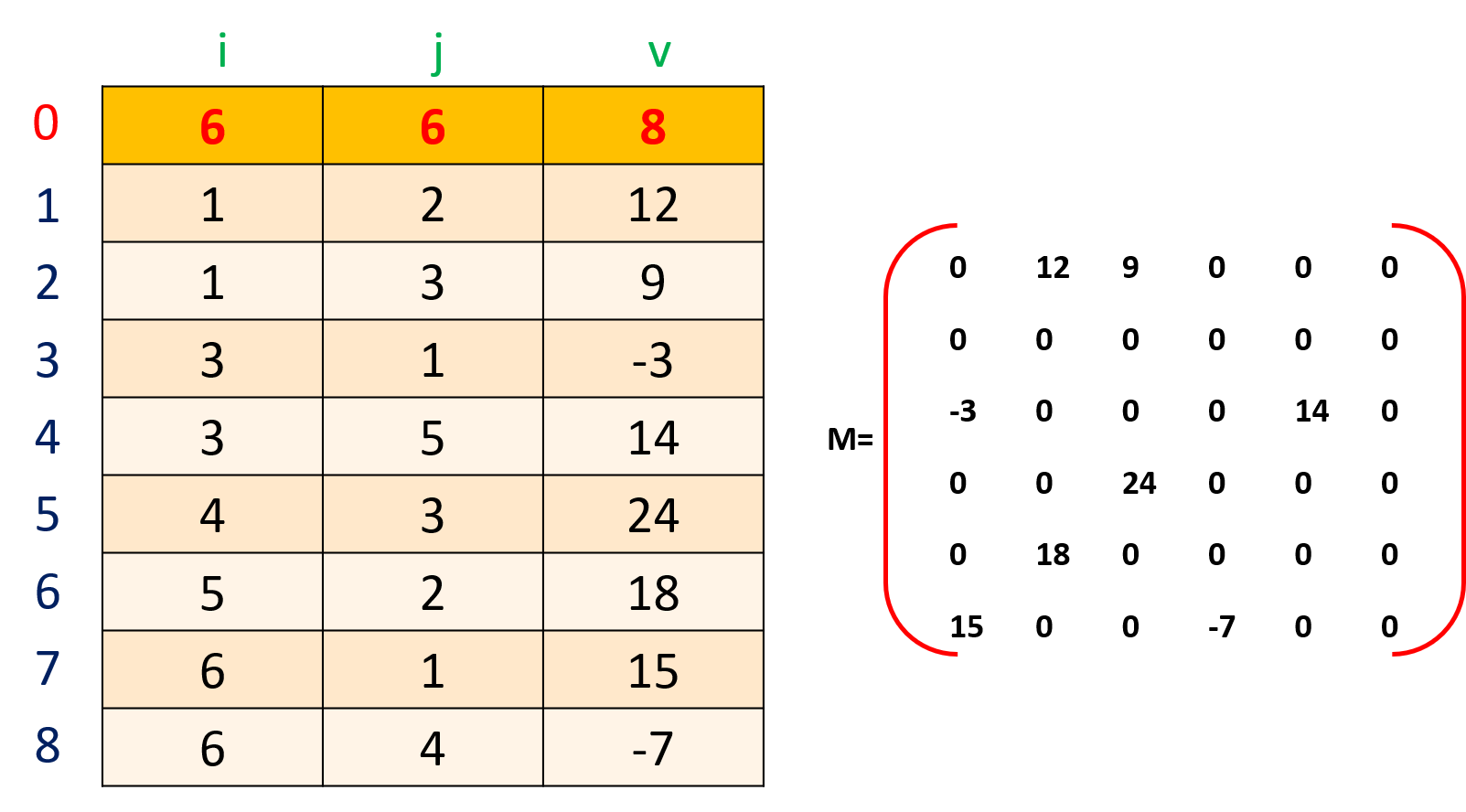
注意:为更可靠描述,通常再加一一个
“总体”信息:即总行数、总列数、非零元素总个数(行下标,列下标,元素值)。
三元组顺序表又称有序的双下标法。
三元组顺序表的优点:非零元在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。
三元组顺序表的缺点:不能随机存取。若按行号存取某一-行中的非
零元,则需从头开始进行查找。
4、三元素组表中的每个结点对应于稀疏矩阵的一个非零元素,它包含有三个数据项,分别表示该元素的____、_____和______。
行下标,列下标,元素值
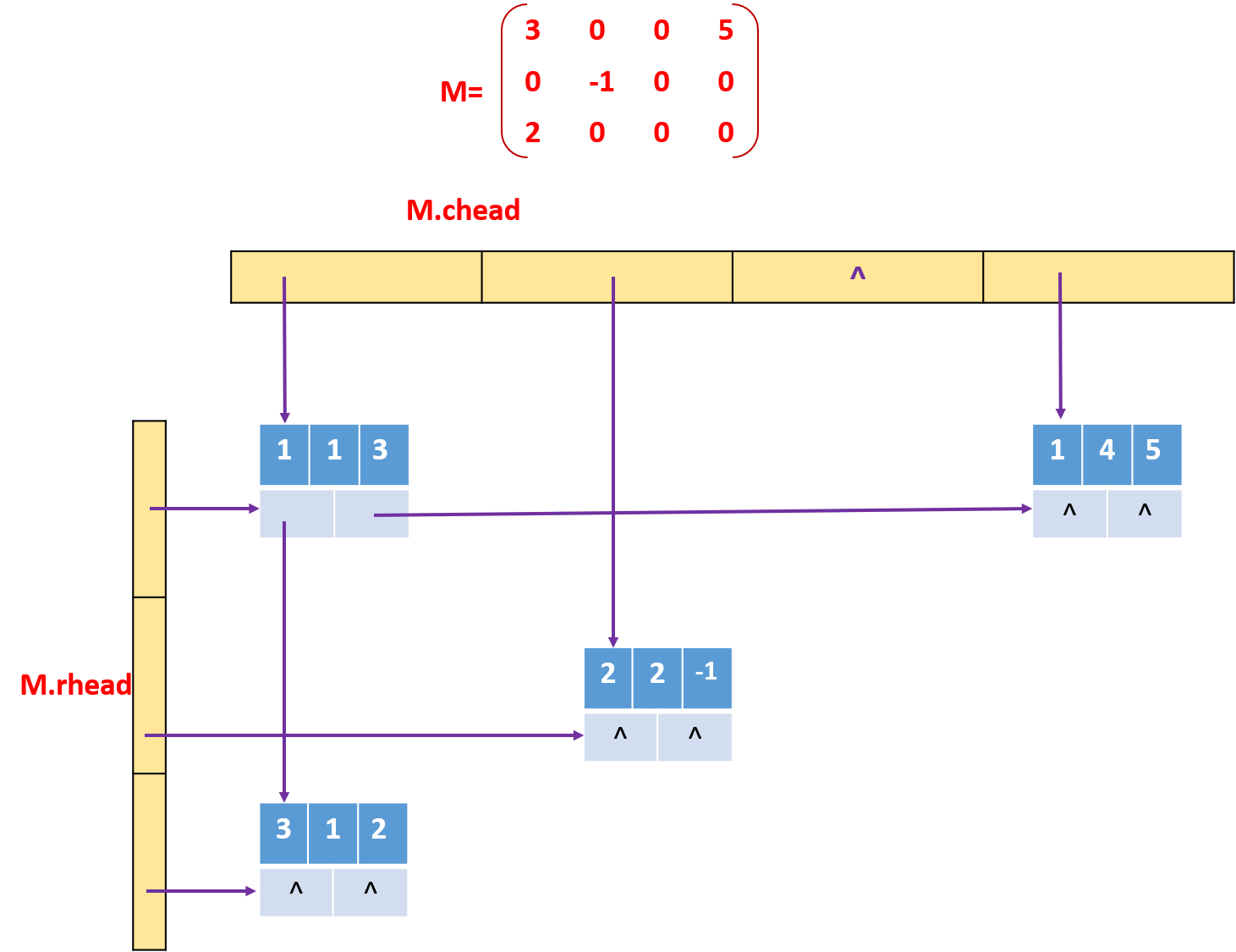
●优点:它能够灵活地插入因运算而产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算。
●在十字链表中,矩阵的每一个非零元素用一一个结点表示,该结点除了(row, col, value) 以外,还要有两个域:
●right: 用于链接同一行中的下一个非零元素;
●down:用以链接同- -列中的下一个非零元素。
●十字链表中结点的结构示意图:
|
row |
col |
value |
|
|
dowm |
right |
||
广义表(又称列表Lists) 是n≥0个元素a0, a1,...., an-1的有限序列,其中每一个 ai或者是原子,或者是一个广义表。
●广义表通常记作: LS=a0, a1,...., an-1
其中: LS为表名, n为表的长度,每一-个a;为表的元素。
●习惯上,一般用大写字母表示广义表,小写字母表示原子。
表头:若LS非空(n≥1), 则其第一个元素a就是表头。
记作head(LS)= a1。注: 表头可以是原子,也可以是子表。
表尾:除表头之外的其它元素组成的表。
记作tail(LS)= (a0, a1,...., an-1)。
注:表尾不是最后-个元素,而是一个子表。
例:
(1) A=() 空表,长度为0。
(2) B=(( )) 长度为1,表头、表尾均为()。
(3) C=(a, (b, d)长度为2,由原子a和子表(b, d)构成。 表头为a;表尾为((b, d)。
(4) D=(x, y, z)长度为3,每一项都是原子。 表头为x表尾为(y, z)。.
(5) E=(C, D)长度为2,每一项都是子表。表头为C;表尾为(D)。
(6) F=(a,F)长度为2,第一项为原子,第二项为它本身.
表头为a;表尾 F=(a, (a, (a, .. .)))
广义表的性质
(1)广义表中的数据元素有相对次序;一个直接前驱和一一个直接后继
(2)广义表的长度定义为最外层所包含元素的个数;
如: C=(a, (b, d)) 是长度为2的广义表。
(3)广义表的深度定义为该广义表展开后所含括号的重数;
A= (b, c)的深度为1,B= (A, d)的深度为2, C= (f, B, h)的深度为3。
注意: "原子” 的深度为0; "空表” 的深度为1。
(4)广义表可以为其他广义表共享;如:广义表B就共享表A。
在B中不必列出A的值,而是通过名称来引用,B= (A)
(5)广义表可以是一个递归的表。如: F=(a,F=(a, (a, (a, …)))
注意:递归表的深度是无穷值,长度是有限值。
(6)广义表是多层次结构,广义表的元素可以是单元素,也可以是子表,而子表的元素还可以是子表,
可以用图形象地表示。
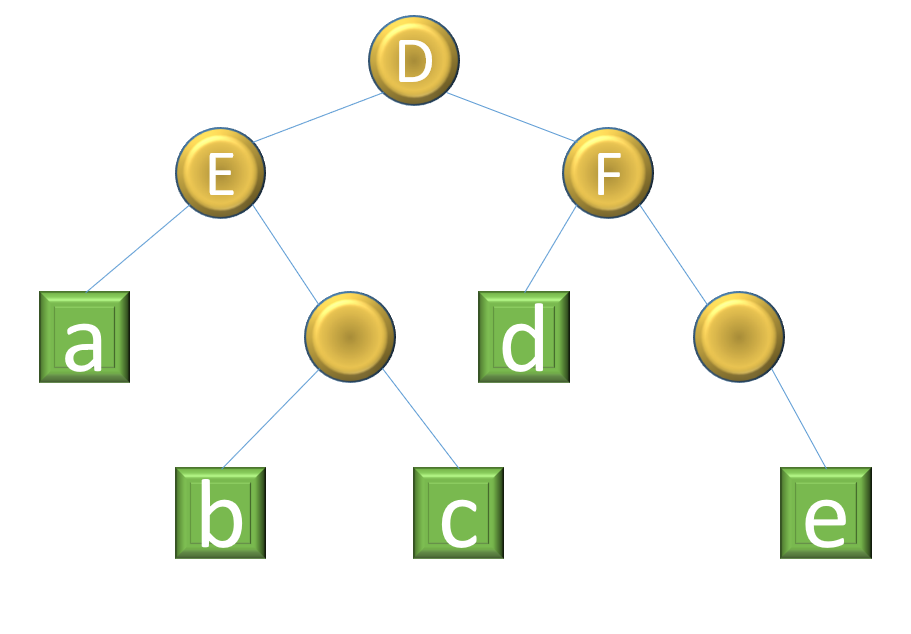
例: D=(E, F)其中:
E=(a, (b, d))F=(d, (e))
广义表与线性表的区别?
广义表可以看成是线性表的推广:,线性表是广义表的特例。
广义表的结构相当灵活,在某种前提下,它可以兼容线性表、数组、
树和有向图等各种常用的数据结构。
当二维数组的每行(或每列)作为子表处理时,二维数组即为一个广
义表。
另外,树和有向图也可以用广义表来表示。
由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的
特点,而且可有效地利用存储空间,因此在计算机的许多应用领域都有成
功使用广义表的实例。
广义表的基本运算
(1)求表头GetHead(L):非空广义表的第一个元素,可以是一个单元个也可以是一个子表
(2)求表尾GetTail(L): 非空广义表除去表头元素以外其它元素所构成的表。表尾一定是一个表
例:
D=( E, F)= ((a,(b, c)), F)
GetHead( D) = E GetTail( D)=( F)
GetHead( E) = a GetTail( E)= ((b, d))
GetHead(((b, c))) = (b, d) GetTai (((b, c))) =()
GetHead((b, c)) = b GetTail ((b, c)) =(c)
GetHead((c)) =(c) GetTail ((c)) =()
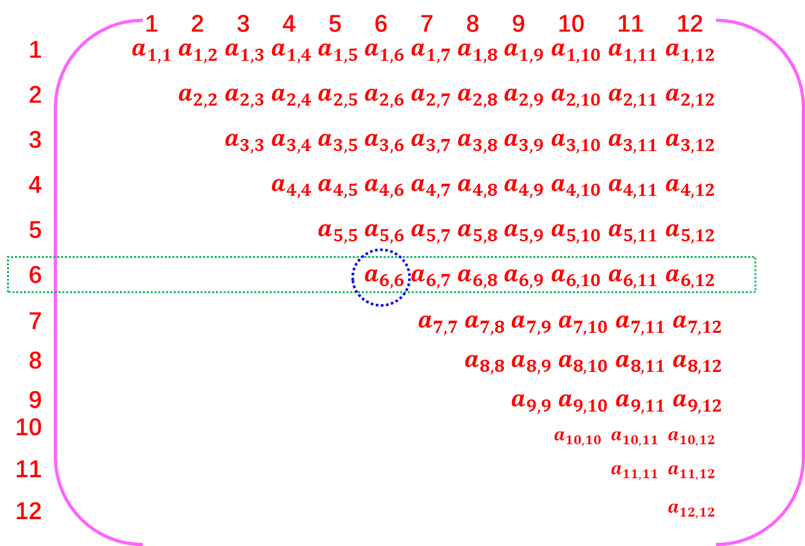
评论列表 (0 条评论)