第八章排序(数据结构)

Chapter8 排序

排序(Sorting)就是将一组杂乱无章的数据按一定的规

律排列起来。本节介绍几种主要的排序方法。

插入排序（直插排序、二分排序、希尔排序）

交换排序（冒泡排序、快速排序）

选择排序（直选排序、树型排序、堆排序）

归并排序（二路归并排序、多路归并排序）

分配排序（多关键字排序、基数排序）

排序的几个基本概念

排序算法的稳定性

关键码相同的数据对象在排序过程中是否保持前后次序不变。如果不变，则该排序方法是稳定的，否则是不稳定的。

排序的时间开销

它是衡量算法好坏的最重要的标志。通常用算法执行中的数据比较次数和数据移动次数来衡量。

学习要点:

⑴排序基本概念及内排序和外排序、稳定排序和非稳定排序的区；

⑵插入排序的基本思想、基本步骤；

⑶冒泡排序的基本思想、基本步骤；

⑷快速排序的基本思想、基本步骤；

⑸直接选择排序的基本思想、基本步骤、算法分析；

⑹堆排序的基本思想、基本步骤；

⑺归并排序的思想；

学习重点:

⑴快速排序算法；

⑵堆排序方法

下面例子在不做说明时，均按升序的方式排序。

8.1 插入排序

插入排序(Insert Sort)的基本原理，每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象适当位置上，直到对象全部插入为止。常见的插入排序方法有：直接插入排序、折半插入排序、Shell排序等。

8.1.1 直接插入排序(Straight Insert Sort)：

⑴、基本思想：

在已形成的有序表中线性查找，并在适当位置插入，把原来位置上的元素向后顺移。

例1：关键字序列T=（13，6，3，31，9，27，5，11），

请写出直接插入排序的中间过程序列。

【13】, 6, 3, 31, 9, 27, 5, 11

【6, 13】, 3, 31, 9, 27, 5, 11

【3, 6, 13】, 31, 9, 27, 5, 11

【3, 6, 13，31】, 9, 27, 5, 11

【3, 6, 9, 13，31】, 27, 5, 11

【3, 6, 9, 13，27, 31】, 5, 11

【3, 5, 6, 9, 13，27, 31】, 11

【3, 5, 6, 9, 11，13，27, 31】

直接插入排序算法的实现：

void InsertSort ( SqList &L ) { //对顺序表L作直接插入排序
    for ( i = 2;  i <=L.length; ++ i ) //直接在原始无序表L中排序
 if (L.r[i].key < L.r[i-1].key) //若L.r[i]较小则插入有序子表内
{ L.r[0]= L.r[i];            //先将待插入的元素放入“哨兵”位置
  L.r[i]= L.r[i-1];         //子表元素开始后移
  for ( j=i-2; L.r[0].key < L.r[j].key; --j ) L.r[j+1]= L.r[j]; 
      //只要子表元素比哨兵大就不断后移
L.r[j+1]= L.r[0];      //直到子表元素小于哨兵，将哨兵值送入
                                 //当前要插入的位置（包括插入到表首）
} //if
}// InsertSort

在对一组记录(54,38,96,23,15,72,60,45,83)进行直接插入排序时,当把第7个记录60插入到有序表时,为寻找插入位置需比较____次

3次

直接插入排序是将待排记录分为有序区和无序区,首先将第一个数做为有序区,然后无序区选择一个数字,

从有序区倒着进行比较。直到无序区没有数字为止(绿色为有序区)

原始序列: 54 38 96 23 15 72 60 45 83选取54作为有序区

第一趟排序:38 54 96 23 15 72 60 45 83 选择38进行比较

第二趟排序:38 54 96 23 15 72 60 45 83 选择96

第三趟排序:23 38 54 96 15 72 60 45 83 选择23,然后从96开始向前比较

第四趟排序:15 23 38 54 96 72 60 45 83 选择15

第五趟排序:15 23 38 54 72 96 60 45 83 选择72

第六趟排序:15 23 38 54 60 72 96 45 83 选择60 60要和96 72 54进行比较

第七趟排序:15 23 38 45 54 60 72 96 83 选择45

第八趟排序:15 23 38 45 54 60 72 83 96 选择83

无序区没有数字,排序完毕,直接插入排序是一种稳定的排序方法,平均时间复杂度O(n^2)

根据选择60那一趟得知,需要比较3次,才能找到合适的插入位置。

例1：关键字序列T= （21，25，49，25*，16，08），
请写出直接插入排序的具体实现过程。

解：假设该序列已存入一维数组r[7]中，将r[0]作为哨兵（Temp）。则程序执行过程为：

时间效率： 因为在最坏情况下，所有元素的比较次数总和为（0＋1＋…＋n-1)→O(n2)。其他情况下也要考虑移动元素的次数。故时间复杂度为O(n2)

空间效率：仅占用1个缓冲单元——O（1）

算法的稳定性：因为25*排序后仍然在25的后面——稳定

折半插入排序

既然子表有序且为顺序存储结构，则插入时采用折半查找定可加速。

优点：比较次数大大减少，全部元素比较次数仅为O(nlog2n)。

时间效率：虽然比较次数大大减少，可惜移动次数并未减少，所以排序效率仍为O(n2) 。

空间效率：仍为 O（1）

稳定性： 稳定

8.1.2 希尔（shell）排序

基本思想：先将整个待排记录序列分割成若干子序列,分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

技巧：子序列的构成不是简单地“逐段分割”，而是将相隔某个增量dk的记录组成一个子序列,让增量dk逐趟缩短（例如依次取5,3,1），直到dk＝1为止。

优点：让关键字值小的元素能很快前移，且序列若基本有序时，再用直接插入排序处理，时间效率会高很多。

算法分析：开始时dk 的值较大，子序列中的对象较少，排序速度较快；随着排序进展，dk 值逐渐变小，子序列中对象个数逐渐变多，由于前面工作的基础，大多数对象已基本有序，所以排序速度仍然很快。

时间效率：O(n^1.25）～O（1.6n^1.25）——由经验公式得到

空间效率：O（1）——因为仅占用1个缓冲单元

算法的稳定性：不稳定——因为49*排序后却到了49的前面

希尔排序算法（主程序）

void   ShellSort(SqList &L，int dlta[ ]，int t){
                //按增量序列dlta[0…t-1]对顺序表L作Shell排序
   for(k=0；k<t；++k)
    ShellInsert(L，dlta[k])； //增量为dlta[k]的一趟插入排序
}  // ShellSort

希尔排序算法（其中某一趟的排序操作）

void   ShellInsert(SqList &L，int dk) {
//对顺序表L进行一趟增量为dk的Shell排序，dk为步长因子
 for(i=dk+1；i<=L.length； ++ i) 
      if(r[i].key < r[i-dk].key) {   //开始将r[i] 插入有序增量子表       
       r[0]=r[i]；  //暂存在r[0] ，此处r[0]仍是哨兵
         for(j=i-dk; j>0&&(r[0].key<r[j].key); j-=dk) 
            r[j+dk]=r[j]；	//关键字较大的记录在子表中不断后移
            r[j+dk]=r[0]； //在本趟结束时将r[i]插入到正确位置
       }//if
} //ShellInsert

8.2、交换排序

交换排序(Exchange Sort)的基本原理，是在待排序的记

录序列中，两两比较待排序记录关键字，并交换不满

足要求的偶对，直到整个序列中的所有记录都满足要

求为止。

常见的选择排序方法有：

冒泡排序、快速排序等

8.2.1 冒泡排序

基本思路：每趟不断将记录两两比较，并按“前小后大”（或“前大后小”）规则交换。

优点：每趟结束时，能挤出一个最大值到最后面位置，一旦下趟没有交换发生，还可以提前结束排序。

前提：顺序存储结构

例：关键字序列 T=(21，25，49，25*，16，08），请写出冒泡排序的具体实现过程。

初态：21，25，49， 25*，16， 08

第1趟：21，25，25*，16， 08 ， 49

第2趟21，25， 16， 08 ，25*，49

第3趟21，16， 08 ，25， 25*，49

第4趟16，08 ，21， 25， 25*，49

第5趟08，16， 21， 25， 25*，49

冒泡排序的算法分析

•最好情况：初始排列已经有序，只执行一趟起泡，做 n-1 次关键码比较，不移动对象。

•最坏情形：初始排列逆序，算法要执行n-1趟起泡，第i趟(1£ i< n) 做了n- i 次关键码比较，执行了n-i 次对象交换。

因此：

时间效率：O（n²) —因为要考虑最坏情况

空间效率：O（1） —只在交换时用到一个缓冲单元

稳定性： 稳定 —25和25*在排序前后的次序未改变

冒泡排序的优点：每一趟整理元素时，不仅可以完全确定一个元素的位置（挤出一个泡到表尾），一旦下趟没有交换发生，还可以提前结束排序。

有没有比冒泡排序更快的算法？

有！

快速排序法——全球公认！

因为它每趟都能准确定位不止1个元素！

8.2.2 快速排序

基本思想：

从待排序列中任取一个元素 (例如取第一个) 作为中心，所有比它小的元素一律前放，所有比它大的元素一律后放，形成左右两个子表；

然后再对各子表重新选择中心元素并依此规则调整，直到每个子表的元素只剩一个。此时便为有序序列了。

优点：因为每趟可以确定不止一个元素的位置，而且呈指数增加，所以特别快！

前提：顺序存储结构

讨论1：如何编程实现？

分析：

①每一趟子表的形成是采用从两头向中间交替式逼近法；

②由于每趟中对各子表的操作都相似，主程序可采用递归算法。

一趟快速排序算法（针对一个子表的操作）

int Partition(SqList &L,int low,int high){ //一趟快排

//交换子表 r[low…high]的记录，使支点（枢轴）记录到位，并返回其位置。返回时，在支点之前的记录均不大于它，支点之后的记录均不小于它。

r[0]=r[low];  //以子表的首记录作为支点记录，放入r[0]单元

pivotkey=r[low].key;  //取支点的关键码存入pivotkey变量


while(low < high){   //从表的两端交替地向中间扫描

  while(low<high && r[high].key>=pivotkey ) - -high;

    r[low]=r[high];  //比支点小的记录交换到低端；

  while(low<high && r[low].key<=pivotkey)  + +low;

    r[high]=r[low];   //比支点大的记录交换到高端；

  }

r[low]=r[0];     //支点记录到位；

  return low;    //返回支点记录所在位置。

}//Partition

整个快速排序的递归算法：

void QSort ( SqList  &L,  int low, int high ) {
//对顺序表L中的子序列r[ low…high] 作快速排序
if ( low < high) {				  
       pivot = Partition ( L, low, high );  //一趟快排，将r[ ]一分为二
       QSort ( L, low, pivot-1);	     //在左子区间进行递归快排，直到长度为1
       QSort ( L, pivot+1, high ); //在右子区间进行递归快排，直到长度为1
    } //if
} //QSort

对顺序表L进行快速排序的操作函数为：

void QuickSort ( SqList  &L) {
   QSort ( L,  1,  L.length );
 }

讨论2. “快速排序”是否真的比任何排序算法都快？

——基本上是，因为每趟可以确定的数据元素是呈指数增加的。

设每个子表的支点都在中间（比较均衡），则：

第1趟比较，可以确定1个元素的位置；

第2趟比较（2个子表），可以再确定2个元素的位置；

第3趟比较（4个子表），可以再确定4个元素的位置；

第4趟比较（8个子表），可以再确定8个元素的位置；

……

只需ëlog2nû ＋1趟便可排好序。

而且，每趟需要比较和移动的元素也呈指数下降，加上编程时使用了交替逼近技巧，更进一步减少了移动次数，所以速度特别快。

教材P276有证明：快速排序的平均排序效率为O(nlog2n)；

1、快速排序的平均时间复杂度是__,它在最坏情况下的时间复杂度是__(要求用大0表示法表示)

o(nlog₂n), o(n²)

8.3 选择排序

选择排序的基本思想是：每一趟在后面n-i 个待排记录中选取关键字最小的记录作为有序序列中的第i 个记录。

选择排序有多种具体实现算法：

1) 简单选择排序

2) 树形选择排序

3) 堆排序

8.3.1 简单选择排序

思路异常简单：每经过一趟比较就找出一个最小值，与待排序列最前面的位置互换即可。

——首先，在n个记录中选择最小者放到r[1]位置；然后，从剩余的n-1个记录中选择最小者放到r[2]位置；…如此进行下去，直到全部有序为止。

优点：实现简单

缺点：每趟只能确定一个元素，表长为n时需要n-1趟

前提：顺序存储结构

例：关键字序列T= （21，25，49，25*，16，08），请给出简单选择排序的具体实现过程。

原始序列： 21，25，49，25*，16，08

第1趟 08，25，49，25*，16，21

第2趟 08，16, 49，25*，25，21

第3趟 08，16, 21，25*，25，49

第4趟 08，16, 21，25*，25，49

第5趟 08，16, 21，25*，25，49

时间效率： O(n2)——虽移动次数较少，但比较次数仍多。

空间效率：O（1）——没有附加单元（仅用到1个temp)

算法的稳定性：不稳定——因为排序时，25*到了25的前面。

简单选择排序的算法如下：

Void SelectSort(SqList  &L ) { //对顺序表L作简单选择排序

    for (i=1;  i<L.length; ++i){
     j = SelectMinKey(L,i); //在r[i…L.length]中选择最小记录并定位
    if( i!=j )  r[i]⟷r[j];  //与第i个记录交换
      } //for
  }  //SelectSort

8.3.2 树形选择排序(又称锦标赛排序)

基本思想：与体育比赛时的淘汰赛类似。

首先对 n 个记录的关键字进行两两比较，得到 én/2ù 个优胜者(关键字小者)，作为第一步比较的结果保留下来。然后在这 én/2ù 个较小者之间再进行两两比较，…，如此重复，直到选出最小关键字的记录为止。

优点：减少比较次数，加快排序速度

缺点：空间效率低

算法分析：

•锦标赛排序构成的树是完全(满）二叉树，其深度为 ëlog2n û +1，其中 n 为待排序元素个数。

•时间复杂度：O(nlog2n) —n个记录各自比较约log2n次

•空间效率： O(n） —胜者树的附加内结点共有n0-1个！

•稳定性：稳定 —可事先约定左结点“小”

讨论：锦标赛排序巧妙利用了第一次和前若干次扫描的结果，加快了排序速度。还有没有同类方法？堆排序

8.3.3 堆排序

堆排序实际上是对树型排序的一个改造，它克服了树型排序所需要的巨大附加空间。

1.什么是堆？

解释：如果让满足以上条件的元素序列（k1，k2，…，kn）顺次排成一棵完全二叉树，则此树的特点是：

树中所有结点的值均大于（或小于）其左右孩子，此树的根结点（即堆顶）必最大（或最小）。

例：有序列T1=（08, 25, 49, 46, 58, 67）和序列T2=（91, 85, 76, 66, 58, 67, 55）,判断它们是否 “堆”？

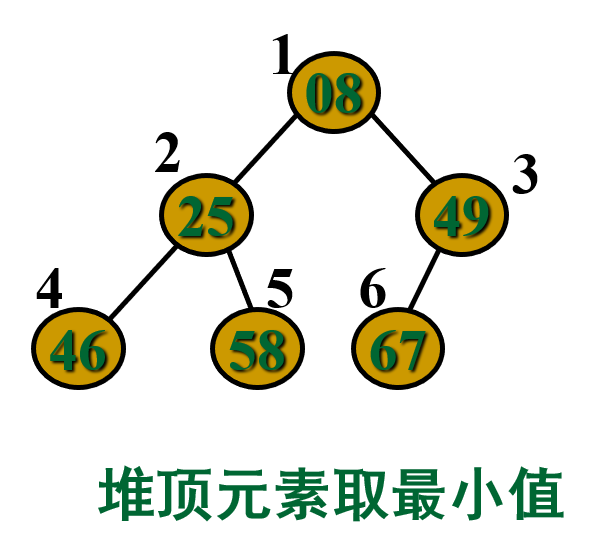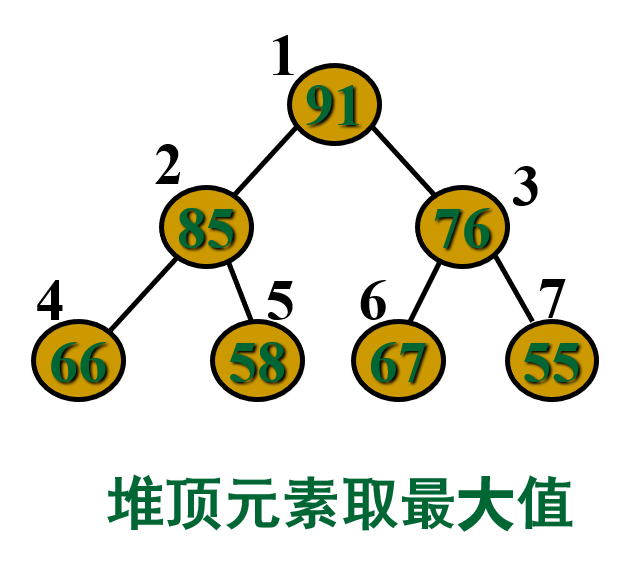2. 怎样建堆？

步骤：从最后一个非终端结点(终端结点（即叶子）没有任何子女，无需单独调整)开始往前逐步调整，让每个双亲大于（或小于）子女，直到根结点为止。

3. 怎样进行整个序列的堆排序？

难点：将堆的当前顶点输出后，如何将剩余序列重新调整为堆？

方法：将当前顶点与堆尾记录交换，然后仿建堆动作重新调整，如此反复直至排序结束。

即：将任务转化为—>

H.r[i…m]中除r[i]外，其他都具有堆特征。

现调整r[i]的值，使H.r[i…m]为堆。

基于初始堆进行堆排序的算法步骤：

堆的第一个对象r[0]具有最大的关键码，将r[0]与r[n]对调，把具有最大关键码的对象交换到最后;

再对前面的n-1个对象，使用堆的调整算法，重新建立堆。结果具有次最大关键码的对象又上浮到堆顶，即r[0]位置;

再对调r[0]和r[n-1]，然后对前n-2个对象重新调整，…如此反复，最后得到全部排序好的对象序列。

堆排序码46，55，13，42，94，05，17，70，建成过程的大根堆后,堆排序过程下图所示。

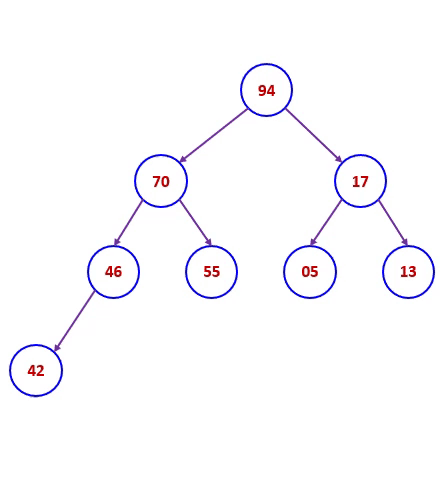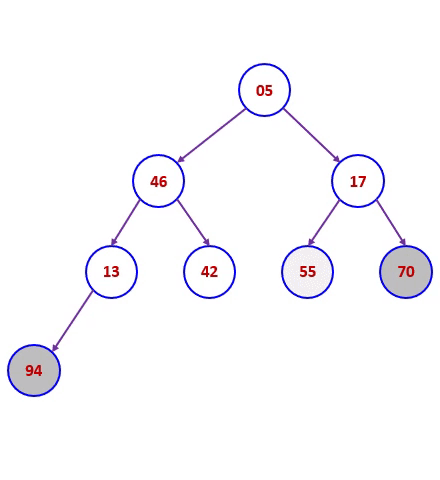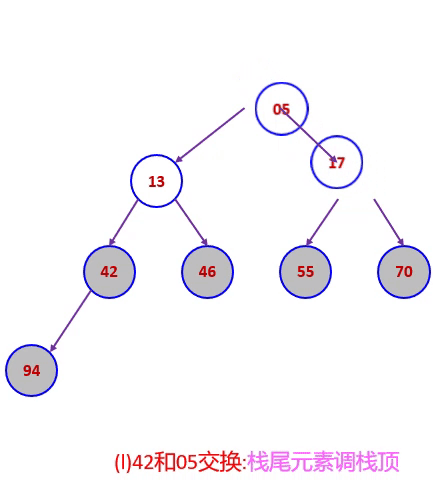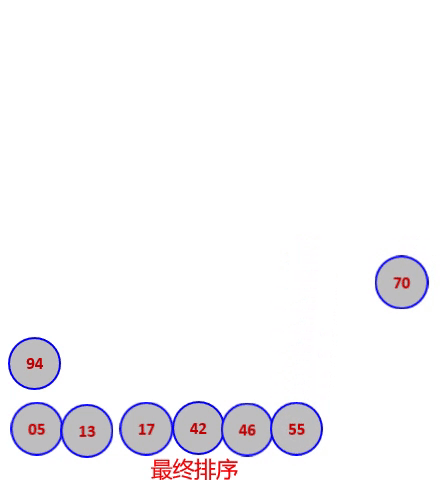
堆排序算法分析：

•时间效率： O(nlog2n)。因为整个排序过程中需要调用n-1次HeapAdjust( )算法，而算法本身耗时为log2n；

•空间效率：O(1)。仅在第二个for循环中交换记录时用到一个临时变量temp。

•稳定性： 不稳定。

•优点：对小文件效果不明显，但对大文件有效。

8.4 归并排序

归并排序的基本思想是：将两个（或以上）的有序表组成新的有序表。

更实际的意义：可以把一个长度为n 的无序序列看成是 n 个长度为 1 的有序子序列 ，首先做两两归并，得到 én / 2ù 个长度为 2 的有序子序列；再做两两归并，…，如此重复，直到最后得到一个长度为 n 的有序序列。

归并排序算法分析：

因为在递归的归并排序算法中，函数Merge( )做一趟两路归并排序，需要调用merge ( )函数 én/(2len)ù » O(n/len) 次，而每次merge( )要执行比较O(len)次，另外整个归并过程有élog2nù “层” ，所以算法总的时间复杂度为O(nlog2n)。

• 空间效率： O(n)

因为需要一个与原始序列同样大小的辅助序列（TR）。这正是此算法的缺点。

• 稳定性：稳定

8.5 基数排序 (Radix Sort)

基数排序的基本思想是：

借助多关键字排序的思想对单逻辑关键字进行排序。即：用关键字不同的位值进行排序。

要讨论的问题：

1. 什么是“多关键字”排序？实现方法？

2. 单逻辑关键字怎样“按位值”排序？

1. 什么是“多关键字”排序？实现方法？

例1：对一副扑克牌该如何排序？

若规定花色和面值的顺序关系为：

面值：2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < J < Q < K < A

则可以先按花色排序，花色相同者再按面值排序；

也可以先按面值排序，面值相同者再按花色排序。

多关键字排序的实现方法通常有两种：

•最高位优先法MSD (Most Significant Digit first)

•最低位优先法LSD (Least Significant Digit first)

例：对一副扑克牌该如何排序？

答：若规定花色为第一关键字（高位），面值为第二关键字（低位），则使用MSD和LSD方法都可以达到排序目的。

MSD方法的思路：先设立4个花色“箱”，将全部牌按花色分别归入4个箱内（每个箱中有13张牌）；然后对每个箱中的牌按面值进行插入排序（或其它稳定算法）。

LSD方法的思路：先按面值分成13堆（每堆4张牌），然后对每堆中的牌按花色进行排序（用插入排序等稳定的算法）。

2. 单逻辑关键字怎样“按位值”排序？

思路：设n 个记录的序列为：{V0, V1, …, Vn-1 }，可以把每个记录Vi 的单关键码 Ki 看成是一个d元组（Ki1, Ki2, …, Kid），则其中的每一个分量K_ij ( 1£ j £ d ) 也可看成是一个关键字。

注1： Ki1＝最高位，Kid＝最低位；Ki共有d位，可看成d元组；

注2： 每个分量Kij (1 £ j £ d ) 有radix种取值，则称radix为基数。

例1：关键码984可以看成是 3 元组；基数radix 为 10

(9, 8, 4) (0, 1, …, 9)

例2：关键码dian可以看成是 4 元组；基数radix 为 26 。

(d, i, a, n) （a, b, …, z）

基数排序算法分析

特点：不用比较和移动，改用分配和收集，时间效率高！

•假设有n 个记录, 每个记录的关键字有d 位，每个关键字的取值有radix个, 则每趟分配需要的时间为O(n)，每趟收集需要的时间为O(radix)，合计每趟总时间为O (n+radix )

全部排序需要重复进行d 趟“分配”与“收集”。因此时间复杂度为：O ( d ( n+radix ) )。

•基数排序需要增加n+2radix个附加链接指针，空间效率低

空间复杂度：O(n+radix）.

•稳定性：稳定。(一直前后有序)。

用途：若基数radix相同，对于记录个数较多而关键码位数较少的情况，使用链式基数排序较好。

8.6 排序总结

下述几种排序方法中，要求内存量最大的是( )。

A．插入排序

B．选择排序

C．快速排序

D．归并排序

正确答案
D

答案解析
A、B、C、D需要的辅助空间分别为：O(1)，O(1)，O(log n)，O(n)。

第八章排序(数据结构)

发表评论

评论列表 (0 条评论)

文章目录

第八章排序(数据结构)

发表评论

评论列表 (0 条评论)

文章目录

模态框头部

登录账号