第六章:图(数据结构)
ADT Graph {
数据对象V:
V是具有相同特性的数据元素的集合,称为顶点集。
数据关系 R:
R={VR};VR={<v,w>|v,w∈V 且 P(v,w),
<v,w>表示从v到w的弧,
谓词P(v,w)定义了弧<v,w>的意义或信息}
基本操作P:
CreatGraph ( &G, V,VR);
初始条件:V是图的顶点集,VR是图中弧的集合。
操作结果:按V和VR的定义构造图G。
InsertVex ( &G, v);
初始条件:图G存在,v 和图中顶点有相同特征。
操作结果:在图G中添加新顶点。
}ADT Graph
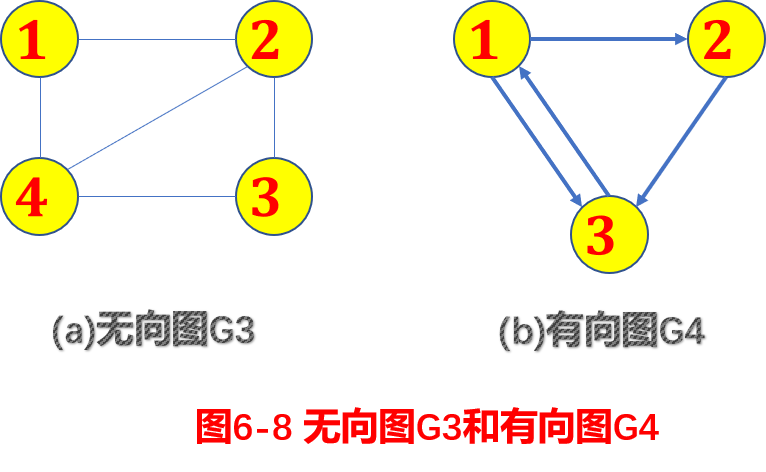
图是由顶点集V和顶点间的关系集合E(边的集合)组成的一种数据结构,可以用二元组定义为:G=(V,E)。
例如,对于图6-1所示的无向图G1和有向图G2,它们的数据结构可以描
述为:G 1 =(V 1 ,E 1 ), 其中 V 1 ={a,b,c,d},E 1 ={(a,b),(a,c),(a,d),(b,d),(c,d)},而
G 2 =(V 2 ,E 2 ),其中V 2 ={1,2,3}, E 2 ={<1,2>,<1,3>,<2,3>,<3,1>}。
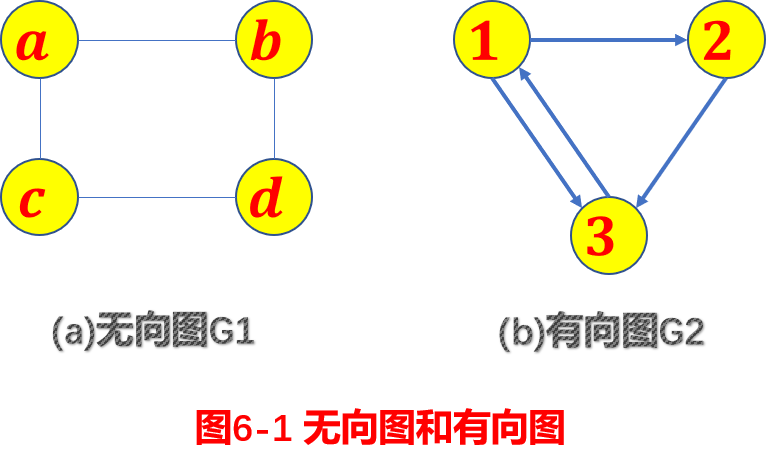
1. 有向图和无向图
在图中,若用箭头标明了边是有方向性的,则称这样的图为有向图,否则称为无向图。
2. 完全图、稠密图、稀疏图和其他术语
具有n个顶点,n(n-1)/2条边的图,称为完全无向图,具有n个顶点,n(n-1)条弧的有向图,称为完全有向图。完全无向图和完全有向图都称为完全图。
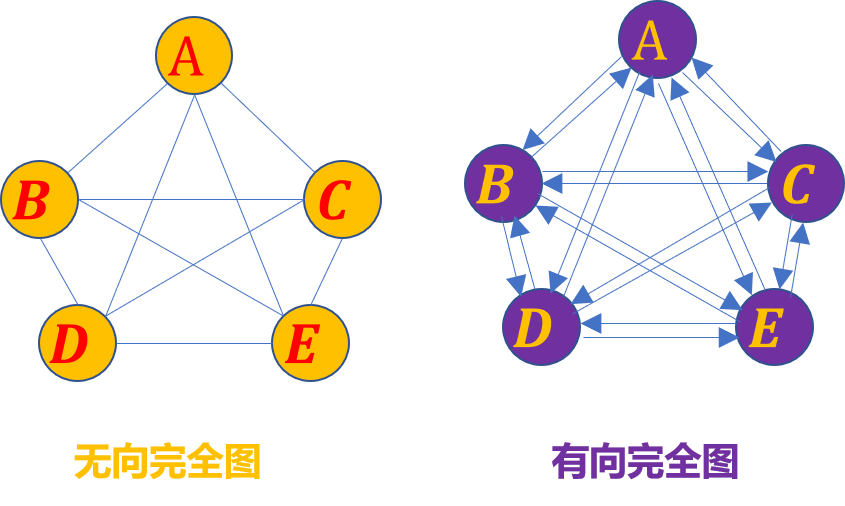
对于一般无向图,顶点数为n,边数为e,则 0≤e ≤n(n-1)/2。
对于一般有向图,顶点数为n,弧数为e, 则 0≤e≤n(n-1) 。
当一个图接近完全图时,则称它为稠密图,相反地,当一个图中含
有较少的边或弧时,则称它为稀疏图。
子图:
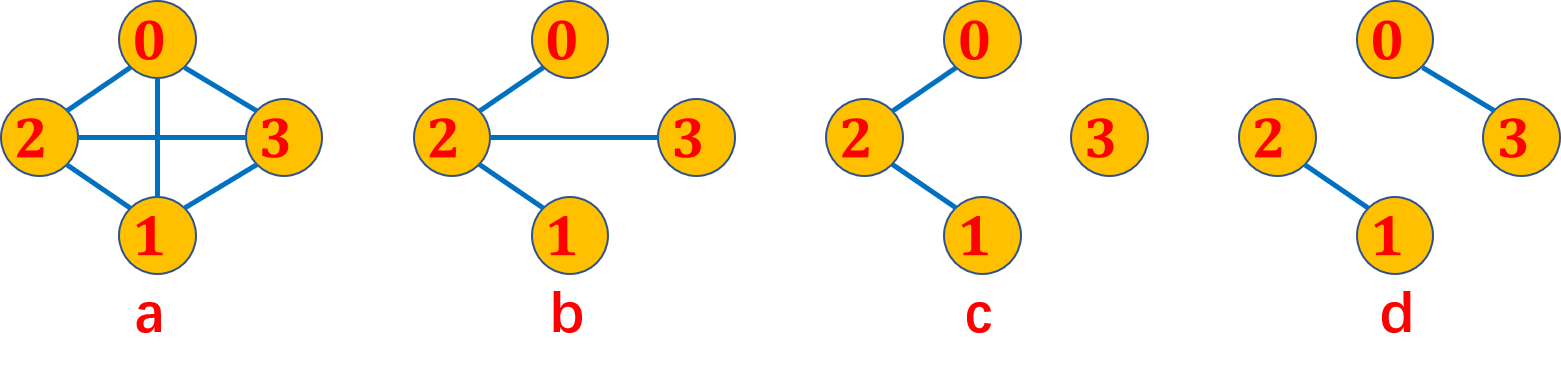
设有两个图 G=(V, E) 和 G’=(V’, E’)。若 V’ Í V 且 E’ ÍE, 则称 图G’ 是 图G 的子图。
下图bcd是a的子图
连通分量(强连通分量)·
无向图G的极大连通子图称为G的连通分量。
极大连通子图意思是:该子图是G连通子图,将G的任何不在该子图中的顶点加入,子图不再连通。
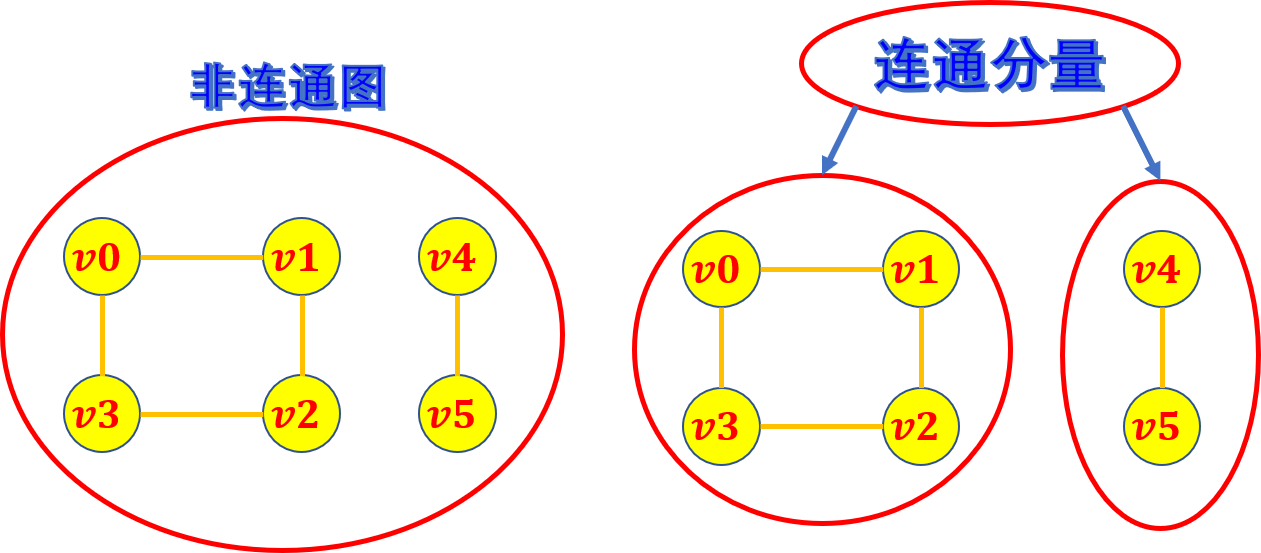
有向图G的极大强连通子图称为G的强连通分量。
极大强连通子图意思是:该子图是G的强连通子图,将D的任何不在该子图中的顶点加入,子图不再是强连通的。
带权图:
即边上带权的图。其中权是指每条边可以标上具有某种含义的数值(即与边相关的数)。
网:→带权图
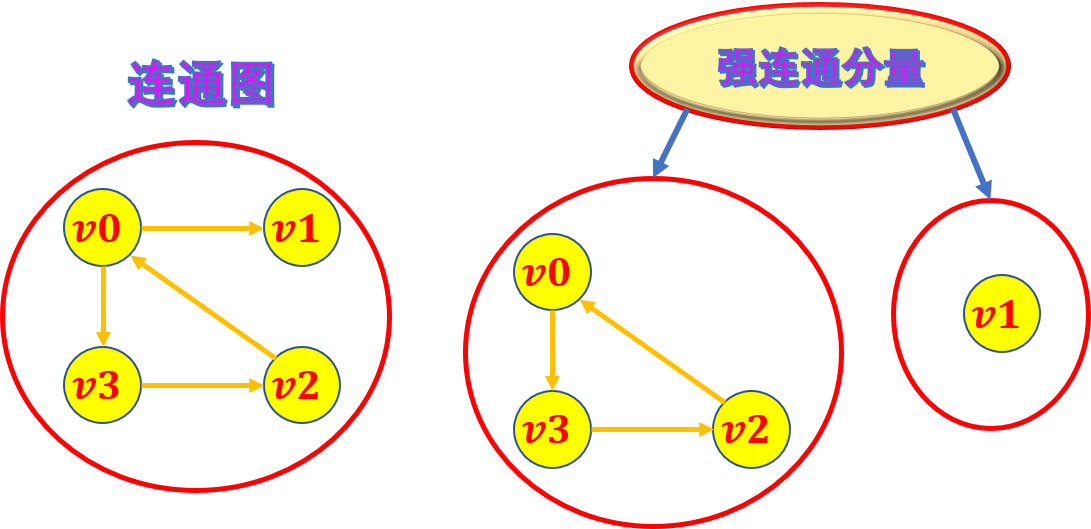
连通图:
在无向图中, 若从顶点v1到顶点v2有路径, 则称顶点v1与v2是连通的。如果图中任意一对顶点都是连通的, 则称此图是连通图。
非连通图的极大连通子图叫做连通分量。
强连通图:在有向图中, 若对于每一对顶点vi和vj, 都存在一条从vi到vj和从vj到vi的路径, 则称此图是强连通图。
非强连通图的极大强连通子图叫做强连通分量。
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,子图不再连通。
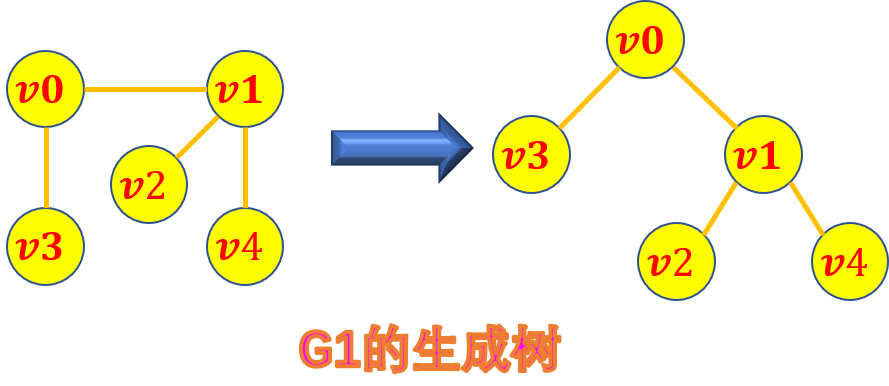
生成树:
是一个极小连通子图,它含有图中全部n个顶点,但只有n-1条边。
- 生成森林:
若干棵生成树的集合,含全部顶点,但构成这些树的边或弧是最少的。
邻接点:
若 (u, v) 是 E(G) 中的一条边,则称 u 与 v 互为邻接顶点。
弧头和弧尾:有向边(u, v)称为弧,边的始点u 叫弧尾,终点v 叫弧头。
路径:在图 G=(V, E) 中, 若从顶点 vi 出发, 沿一些边经过一些顶点 vp1, vp2, …, vpm,到达顶点vj。则称顶点序列 ( vi vp1 vp2 ... vpm vj ) 为从顶点vi 到顶点 vj 的路径。它经过的边(vi, vp1)、(vp1, vp2)、...、(vpm, vj)应当是属于E的边。
路径长度:
非带权图的路径长度是指此路径上边的条数;
带权图的路径长度是指路径上各边的权之和。
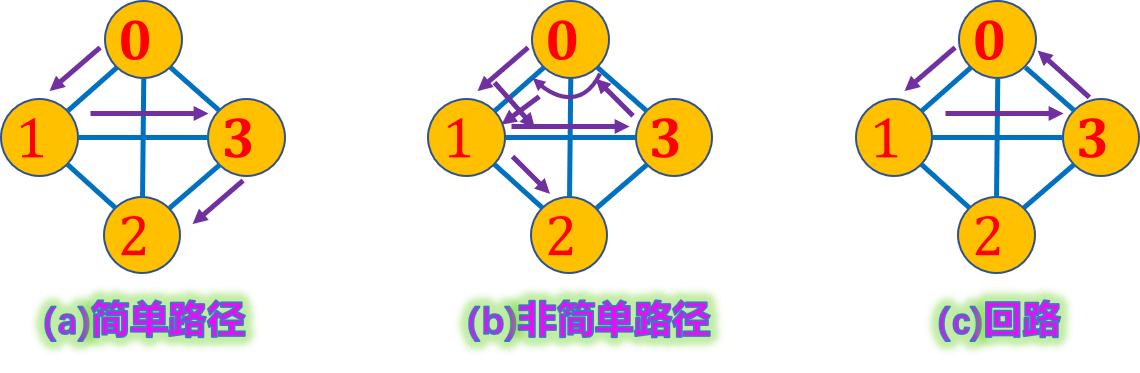
简单路径:
路径上各顶点 v1,v2,...,vm 均不互相重复。
回路:
若路径上第一个顶点 v1 与最后一个顶点vm 重合,则称这样的路径为回路或环。
3. 度、入度、出度
在图中,一个顶点依附的边或弧的数目,称为该顶点的度。在有向图中,一个顶点依附的弧头数目,称为该顶点的入度。一个顶点依附的弧尾数目,称为该顶点的出度,某个顶点的入度和出度之和称为该顶点的度。
若图中有n个顶点,e条边或弧,第i个顶点的度为di ,则有
\(e=\sum_{i=1}^{n} d_i\)
| 17、有8个结点的无向图最多有多少条边() |
| A.14 |
| B.28 |
| C.56 |
| D.58 |
| B |
|
选B.每2个结点间有bai一条边,因此8个结点最多有C(8, 2)条边zhi 直观来说,若一个图中每条边都是无方向的,则称为无向图。 (1)无向边的表示 无向图中的边均是顶点的无序对,无序对通常用圆括号表示。 【例】无序对(vi,vj)和(vj,vi)表示同一条边。 (2)无向图的表示 【例】下面(b)图中的G2和(c)图中的G3均是无向图,它们的顶点集和边集分别为: V(G2)={v1,v2,v3,v4} E(G2)={(vl,v2),(v1,v3),(v1,v4),(v2,v3),(v2,v4),(v3,v4)} V(G3)={v1,v2,v3,v4,v5,v6,v7} E(G3)={(v1,v2),(vl,v3),(v2,v4),(v2,v5),(v3,v6),(v3,v7)}
|
|
26.数据结构第五章:图.第一节:图得基本概念第178页,第一,7题 7.[2010年计算机联考真题] |
| A.6 |
| B.15 |
| C.16 |
| D.21 |
| C |
| 7.C,题目要求在"任何情况"下都是连通的,考虑最极端的情形,即图G的6个顶点构成一个完全无向图,在加上一条边后,第7个顶点必然与完全无向图构成一个连通图,所以最少边数=6*5/2+1=16,若边数n小于或等于15时,可以使这n条边仅链接图G中的某6个点,从而导致第7个顶点无法与这6个顶点构成连通图(不满足"任何情况"). |
1.图的邻接矩阵表示
在邻接矩阵表示中,除了存放顶点本身信息外,还用一个矩阵表示各个顶点之间的关系。若(i,j)∈E(G)或〈i,j〉∈E(G),则矩阵中第
i行第j列元素值为1,否则为0 。
图的邻接矩阵定义为:
\(\color{red}{A[i][j]=} \begin{cases} 1 , 若(i,j)∈E(G)或<i, j>∈E(G)\\ 其他情形\\ \end{cases}\)
例如, 对图6-8所示的无向图和有向图,它们的邻接矩阵见图6-9。
|
\(\begin{pmatrix} 0& 1 &0 &1\\ 1& 0& 1&1\\ 0& 1&0&1\\ 1& 1&1&0 \end{pmatrix} \) (a) G3的邻接矩阵 |
\(\begin{pmatrix} 0& 1&1 \\ 0& 0& 1\\ 1& 0&0 \end{pmatrix}\) (b) G4 的邻接矩阵 |
图6-9邻接矩阵表示
2.从无向图的邻接矩阵可以得出如下结论
(1)矩阵是对称的;
(2)第i行或第i 列1的个数为顶点i 的度;
(3)矩阵中1的个数的一半为图中边的数目;
(4)很容易判断顶点i 和顶点j之间是否有边相连(看矩阵中i行j列值是否为1)。
3. 从有向图的邻接矩阵可以得出如下结论
(1) 矩阵不一定是对称的;
(2) 第i 行中1的个数为顶点i 的出度;
(3) 第i列中1的个数为顶点i的入度;
(4) 矩阵中1的个数为图中弧的数目;
(5) 很容易判断顶点i 和顶点j 是否有弧相连.
4.网的邻接矩阵表示
类似地可以定义网的邻接矩阵为:
\(\color{red}{A[i][j]=} \begin{cases} w_{ij},&若{i,j}∈E(G)或<i,j>∈E(G)\\ 0, &若i=j\\ ∞, &其他\\ \end{cases}\)
|
|
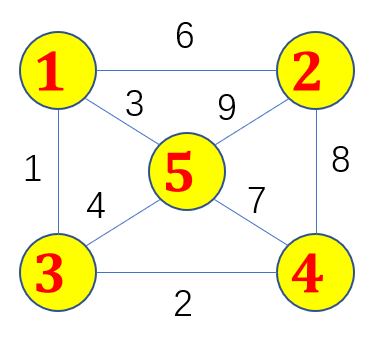
\(\begin{pmatrix} ∞& 6 &1 &∞ & 3\\ 6& ∞& ∞&8 & 9\\ 1& ∞ & ∞ &2 & 4\\ ∞& 8 & 2 & ∞ & 7 \\ 3 & 9 & 4 & 7& ∞ \end{pmatrix} \) |
| (a)网G5 | (b)网G5的邻接矩阵示意图 |
|
图6-10网及邻接矩阵示意图 |
|
5.图的邻接矩阵数据类型描述
图的邻接矩阵数据类型描述如下:
struct mgraph
{
图中顶点数;
图中边数;
存放顶点信息v1,v2,….vn;
邻接矩阵;
};
|
74.数据结构王道最后8套题第七套第一,7题050页 7.以下关于图的叙述中,正确的是( )。 |
| A.强连通有向图的任何顶点到其他所有顶点都有弧 |
| B.图与树的区别在于图的边数大于或等于顶点数 |
| C.无向图的连通分量指无向图中的极大连通子图 |
| D.假设有图 G={V,{E}},顶点集V′ ⊆V,E′ ⊆E,则V′和{E′}构成G 的子图 |
| C |
|
7.C。 【解析】考查图的基本性质。强连通有向图的任何顶点到其他所有顶点都有路径,但未必有弧,A 错误。图与树的区别是逻辑上的,而不是边数的区别,图的边数也可能小于树的边数。若 E′中的边对应的顶点不是 V′中的元素时,则 V′和{E′}无法构成图,D 错误。 |
|
表结点 |
|
头结点 |
|||
|
adjvex |
wright |
next |
info |
first |
|
把同一个顶点发出的边链接在同一个边链表中 , 链表的每一个结点代表一条边,叫做表结点(边结点),邻接点域 adjvex, 链 保存与该边相关联的另一顶点的顶点下标 , 链域 next 存放指向同一链表中下一个表结点的指针 ,数据域存放指向同一链表中下一个表结点的指针 ,数据域 weight 存放边的权。边链表的表头指针存放在头结点中。头结点以顺序结构存储,其数据域存放边的权。边链表的表头指针存放在头结点中。头结点以顺序结构存储,其数据域 info 存放顶点信息,链域 first 指向链表中第一个顶点

2.从无向图的邻接表可以得到如下结论
(1)第i 个链表中结点数目为顶点i的度;
(2)所有链表中结点数目的一半为图中边数;
(3)占用的存储单元数目为n+2e
3.从有向图的邻接表可以得到如下结论
(1)第i 个链表中结点数目为顶点i的出度;
(2)所有链表中结点数目为图中弧数;
(3)占用的存储单元数目为n+e 。
从有向图的邻接表可知,不能求出顶点的入度。为此,我们必须另外建立有向图的逆邻接表,以便求出每一个顶点的入度。逆邻接表在图6-11(c)中已经给出,从该图中可知。有向图的逆邻接表与邻接表类似,只是它是从入度考虑结点,而不是从出度考虑结点。
|
|
||
|
适用稠密图 |
适用性 |
适用稀疏图 |
|
顺序存储 |
存储方式 |
顺序存储+链式存储 |
|
效率高 |
判断两顶点间是否存在边 |
效率低 |
|
效率低 |
找出某顶点相邻的边 |
效率高 |
8、稠密图适合采用____存储结构。
邻接矩阵
| 在图采用邻接表存储时,求最小生成树的 Prim 算法的时间复杂度为( ). |
| A. O(n) |
| B. O(n+e) |
| C. O(n2) |
| D. O(n3) |
| B |
|
B. 邻接表储存时,是B.邻接矩阵储存就是C了 |
从图中某一顶点出发访遍图中其余顶点,且使每个顶点仅被访问一次,就叫做图的遍历(Traversing Graph)。
图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。
两条遍历图的路径:深度优先搜索(栈)、广度优先搜索(队列)
|
74.计算机组成原理王道最后8套题第四套第一,9题025页 9.下列可用于表示有向图的存储结构有( )。 I. 邻接矩阵 II. 邻接表 III.十字链表 IV.邻接多重表 |
| A. I和II |
| B. II和IV |
| C.I、II和III |
| D.I、II和IV |
| D |
|
9. D. [解析]考查图的存储结构。邻接矩车和邻接表既能存储有向图,也能存储无向图,邻接多重衣只能存储有向图,十字链表只能存储无向图,I、II和IV符合题意,选D. |
深度优先搜索遍历类似于树的先序遍历。
则深度优先搜索遍历算法执行如下:
(1) 首先访问顶点i,并将其访问标记置为访问过,即visited[i]=1;
(2) 然后搜索与顶点i有边相连的下一个顶点j,若j未被访问过,则访问它,并将j的访问标记置为访问过,visited[j]=1,然后从j开始重复此过程,若j已访问,再看与i有边相连的其它顶点;
(3) 若与i有边相连的顶点都被访问过,则退回到前一个访问顶点并重复刚才过程,直到图中所有顶点都被访问完止。
深度优先搜索遍历类似于树的先序遍历。
则深度优先搜索遍历算法执行如下:
(1) 首先访问顶点i,并将其访问标记置为访问过,即visited[i]=1;
(2) 然后搜索与顶点i有边相连的下一个顶点j,若j未被访问过,则访问它,并将j的访问标记置为访问过,visited[j]=1,然后从j开始重复此过程,若j已访问,再看与i有边相连的其它顶点;
(3) 若与i有边相连的顶点都被访问过,则退回到前一个访问顶点(栈的方式)并重复刚才过程,直到图中所有顶点都被访问完止。
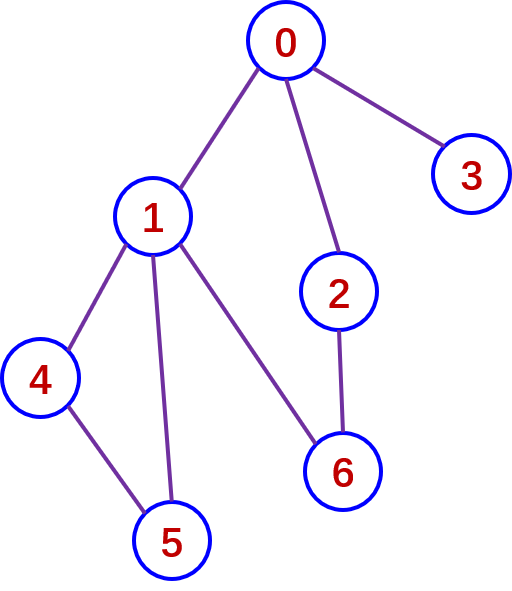
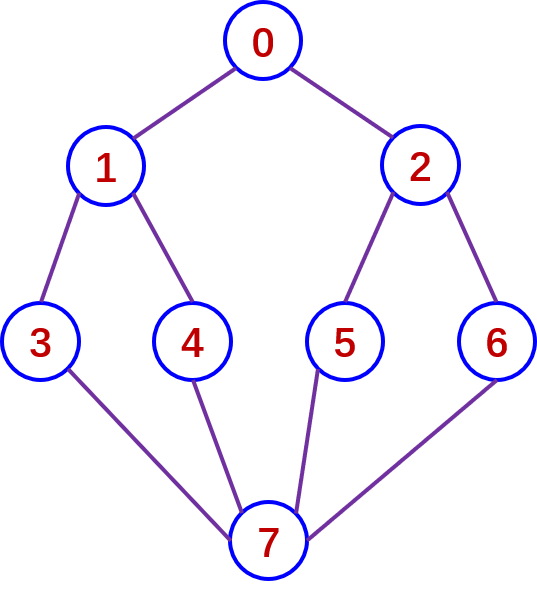
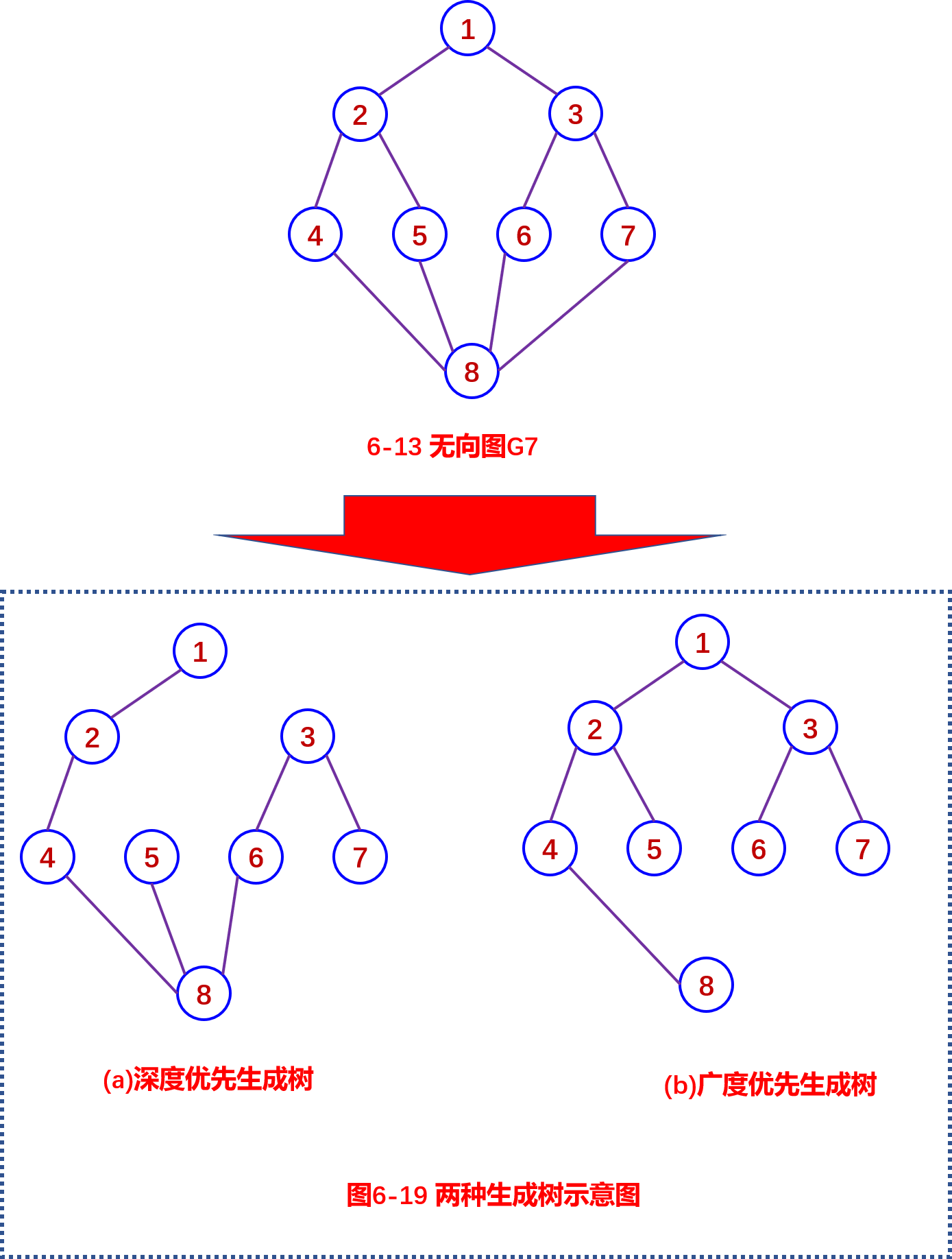
例如,对图6-13所示无向图G7,从顶点1出发的深度优先搜索遍
历序列可有多种,下面仅给出三种,其它可作类似分析。
在无向图G7中,从顶点1出发的深度优先搜索遍历序列举如下:
 |
 |
|
6-13无向图G7 |
6-13无向图G8 |
例如,对图6-13所示无向图G7,从顶点1出发的深度优先搜索遍
历序列可有多种,下面仅给出三种,其它可作类似分析。
在无向图G7中,从顶点0出发的深度优先搜索遍历序为:
0,3,2,6,1,5,4

1. 广度优先搜索的思想
按上述所说,采用队列是合适的。
⑴开始时要将其置空。
⑵在每访问一个顶点时,要将其入队。
⑶在访问一个顶点的所有后继时,要将其出队。
⑷若队列为空时,说明每一个访问过的顶点的所有后继均已访问完毕,因而本次遍历可以结束。若此时还有未访问的顶点,需要另选起点进行遍历。
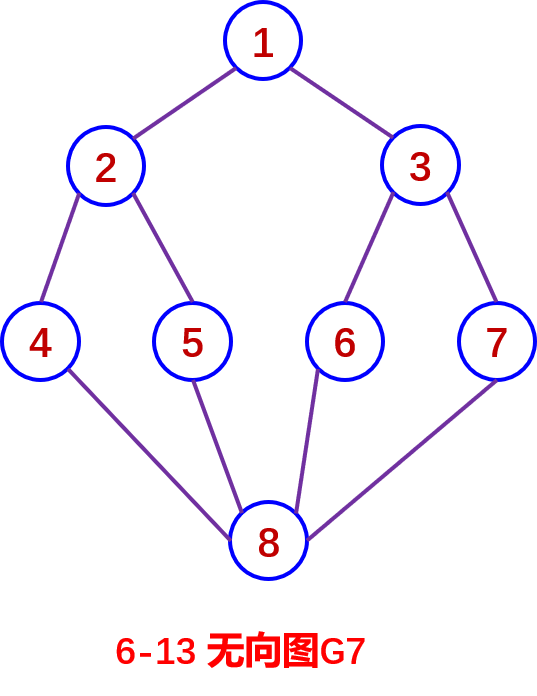
例如,对图6-13所示无向图G7,从顶点1出发的广度优先搜索遍
历序列可有多种,下面仅给出三种,其它可作类似分析。
在无向图G7中,从顶点1出发的广度优先搜索遍历序列举如下:
例如,对图6-13所示无向图G7,从顶点1出发的广度优先搜索遍
历序列可有多种,下面仅给出三种,其它可作类似分析。
在无向图G7中,从顶点1出发的广度优先搜索遍历序列举三种
为:
1 2 3 4 5 6 7 8
1, 2, 3, 4, 5, 6, 7, 8
1, 3, 2, 7, 6, 5, 4, 8
1, 2, 3, 5, 4, 7, 6, 8
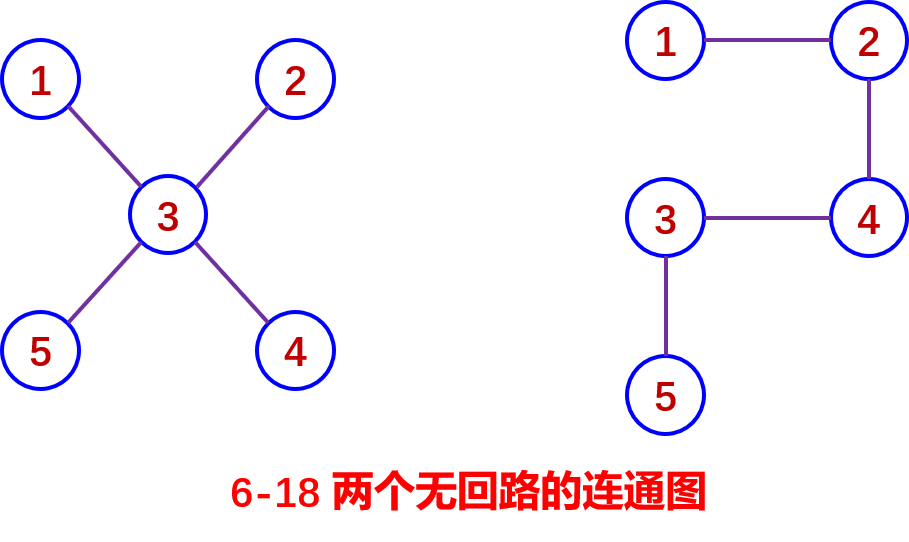
1. 生成树
在图论中,常常将树定义为一个无回路连通图。例如,图6-18中的两个图就是无回路的连通图。乍一看它似乎不是不是树,但只要选以边,可以它 定某个顶点做根并 树根为起点对每条 定向 就 将 们变为通常的树。
|
74.数据结构王道最后8套题第五套第一,7题033页 7.如果具有n个顶点的图是一个环,则它有( ) 棵生成树。 |
| A. n² |
| B. n |
| C. n-1 |
| D. 1 |
| B |
|
7. B。 [解析1考查图的生成树。n个顶点的生成树是具有n-1条边的极小连通子图,n个顶点构的环具有n条边,去掉任一条边后剩下的图依然 是连通的。因为n个项点构成的环共有n条边,去掉其中任意一条便是一棵生成树, 共有n种情况,所以可以有n棵不同的生成树(如,以n=3为例读者自行分析)。 |
2.最小生成树
在一般情况下,图中的每条边若给定了权,这时,我们所关心的不是生成树,而是生成树中边上权值之和。若生成树中每条边上权值之和达到最小,称为最小生成树。
下面将介绍求最小生成树的两种方法:普里姆算法和克鲁斯卡尔算法。
|
74.计算机组成原理王道最后8套题第四套第一,6题025页 6.在具有n个顶点的图G中,若最小生成树不唯一,则() |
| A.G的边数一定大于n-1 |
| B. G的权值最小的边一定有多条 |
| C. G的最小生成树代价不一定相等 |
| D.上述选项都不对 |
| A |
| 6.A 解析1G的最小生成树的边数为n-1,若最小生成树不唯,则G的边数定大于n-1, A正确。在G中找到与最小生成树T中某条边e1权值相等的边e2,加入最小生成树中,则会产生一个环,就可以用e2来代替e1,形成一个 新的最小生成树E,=T-e1+e2,这就使最小生成树不唯一,而边的权值在这里是任意的,并不是最小的,B错误。最小生成树的树形可能不唯一, 但代价肯定是相等且是最小的,C错误。 |
1.普里姆(prim)算法思想
下面仅讨论无向网的最小生成树问题。
普里姆方法的思想是:在图中任取一个顶点K作为开始点,令U={k},W=V-U,其中V为图中所有顶点集,然后找一个顶点在U中,另一个顶点在W中的边中最短的一条,找到后,将该边作为最小生成树的树边保存起来,并将该边顶点全部加入U集合中,并从W中删去这些顶点,然后重新调整U中顶点到W中顶点的距离, 使之保持最小,再重复此过程,直到W为空集止。
用Prim算法给出图G的一棵最 小生成树的生成过程
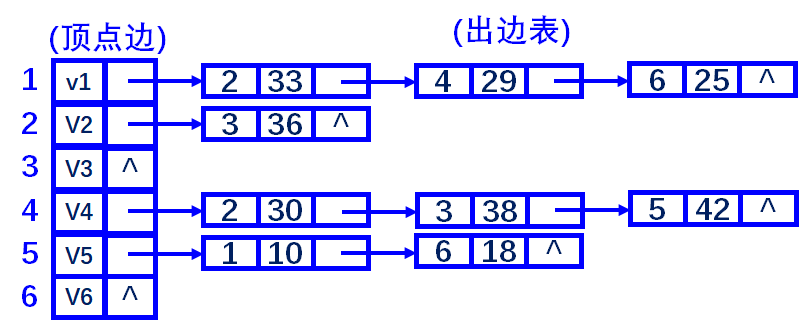
从V1点开始,第一趟寻找V1和点集{V2,V3,V4,V5,V6}之间的最小权值的边。(V5,V1)。
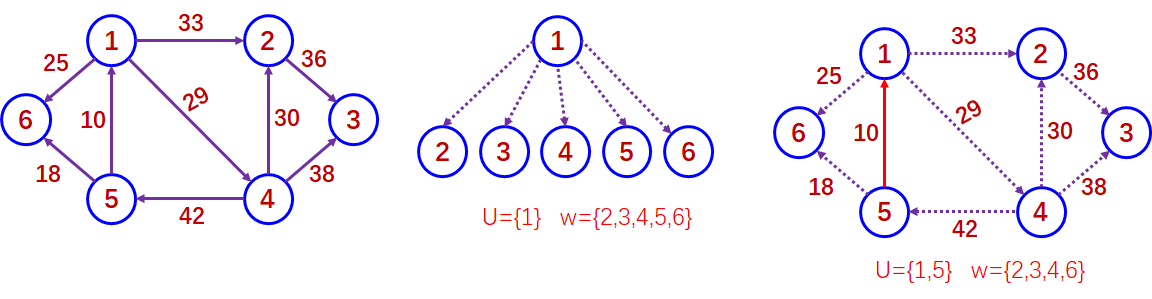
第二趟寻找点集{V1,V5}和点集{V2,V3,V4,V6}之间的最小权值的边。(V5,V6)。
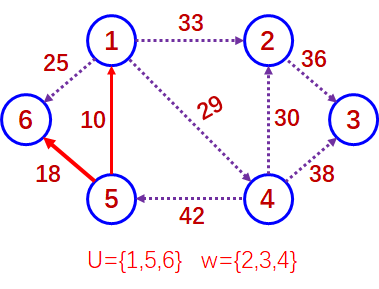
第三趟寻找点集{V1,V5,V6}和点集{V2,V3,V4}之间的最小权值的边。(V1,V4)。
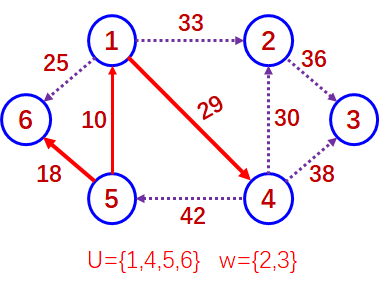
第四趟寻找点集{V1,V4,V5,V6}和点集{V2,V3}之间的最小权值的边。(V4,V2)。
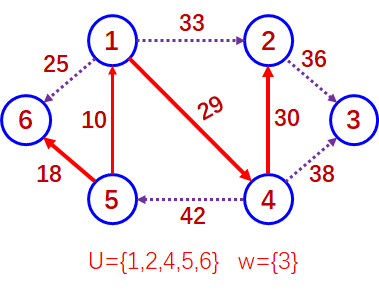
第五趟寻找点集{V1,V2,V4,V5,V6}和点集{V3}之间的最小权值的边。(V2,V3)。
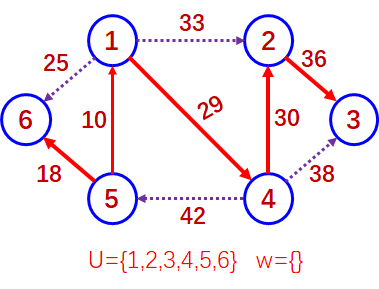
所以最小生成树的边集合为{(V5,V1), (V5,V6), (V1,V4), (V4,V2),(V2,V3)}
1. 克鲁斯卡尔算法基本思想
克鲁斯卡尔算法的基本思想是:将图中所有边按权值递增顺序排列,依次选定取权值较小的边,但要求后面选取的边不能与前面选取的边构成回路,若构成回路,则放弃该条边,再去选后面权值较大的边,n个顶点的图中,选够n-1条边即可。
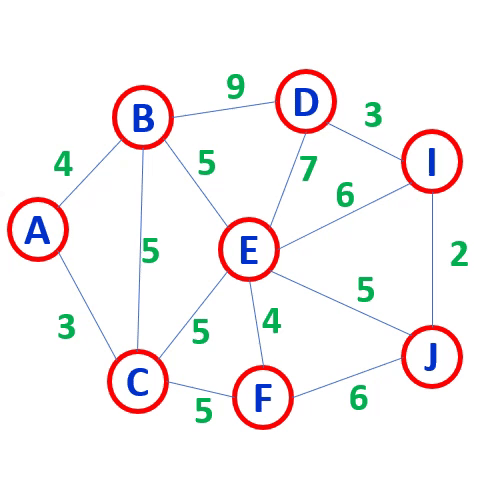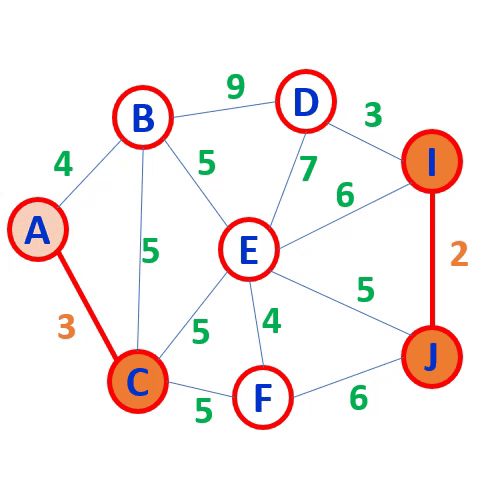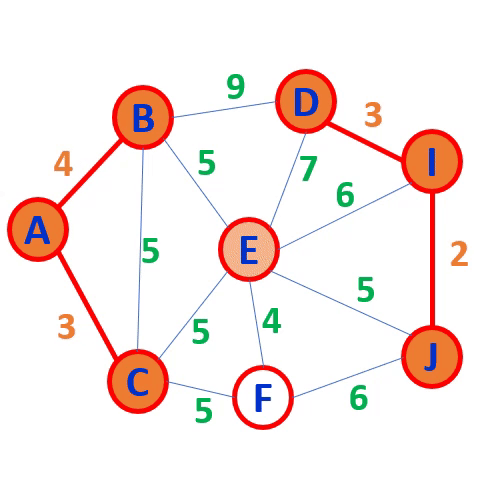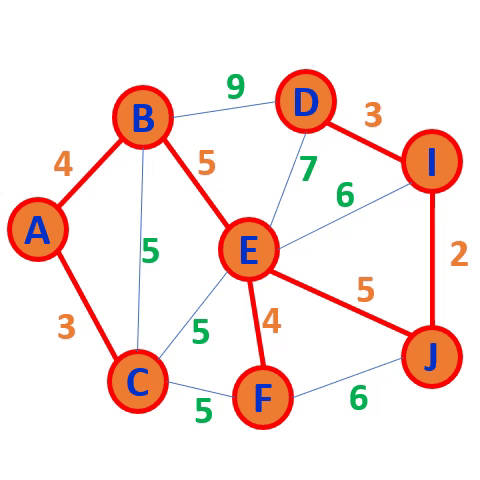
例如,对图6-20(a) 中无向网,用克鲁斯卡尔算法求最小生成树的过程见图6-22。
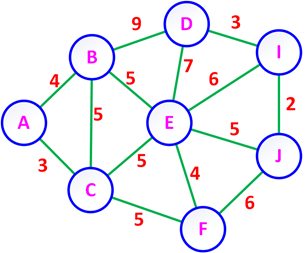
克鲁斯卡尔(kruskal) 算法:
按权值递增的顺序,
适合稀疏矩阵
不能形成回路
|
算法名 |
算法思想 |
时间复杂度 |
适应范围 |
|
普里姆算法 |
选择点 |
O(n2)(n为顶点数) |
稠密图 |
|
克鲁斯卡尔算法 |
选择边 |
O(eloge)(e为边数) |
稀疏图 |
交通网络中常常提出这样的问题:从甲地到乙地之间是否有公路连通?在有多条通路的情况下,哪一条路最短? 交通网络可用带权图来表示。顶点表示城市名称,边表示两个城市有路连通,边上权值可表示两城市之间的距离、交通费或途中所花费的时间等。求两个顶点之间的最短路径,不是指路径上边数之和最少,而是指路径上各边的权值之和最小。
另外,若两个顶点之间没有边,则认为两个顶点无通路,但有可能有间接通路(从其它顶点达到)。路径上的开始顶点(出发点)称为源点,路径上的最后一个顶点称为终点,并假定讨论的权值不能为负数。
1.单源点最短路径
单源点最短路径是指:给定一个出发点(单源点)和一个有向网G=(V,E),
求出源点到其它各顶点之间的最短路径。
那么怎样求出单源点的最短路径呢?我们可以将源点到终点的所有路径都列出来,然后在里面选最短的一条即可。但是这样做,用手工方式可以,当路径特别多时,显得特别麻烦,并且没有什么规律,不能用计算机算法实现。
迪杰斯特拉(Dijkstra)在做了大量观察后,首先提出了按路长度递增序产生各顶点的最短路径算法,我们称之为迪杰斯特拉算法。
2. 迪杰斯特拉算法的基本思想
算法的基本思想是:设置并逐步扩充一个集合S,存放已求出其最短路径的顶点,则尚未确定最短路径的顶点集合是V-S,其中V为网中所有顶点集合。按最短路径长度递增的顺序逐个以V-S中的顶点加到S中,直到S中包含全部顶点,而V-S为空。
具体做法是:设源点为Vl,则S中只包含顶点Vl,令W=V-S,则W中包含除Vl外图中所有顶点,Vl对应的距离值为0,W中顶点对应的距离值是这样规定的:若图中有弧<Vl,Vj>则Vj顶点的距离为此弧权值,否则为∞(一个很大的数),然后每次从W中的顶点中选一个其距离值为最小的顶点Vm加入到S中,每往S中加入一个顶点Vm,就要对W中的各个顶点的距离值进行一次修改。若加进Vm做中间顶点,使<Vl,Vm>+<Vm,Vj>的值小于<Vl,Vj>值,则用<Vl,Vm>+<Vm,Vj>代替原来Vj的距离,修改后再在W中选距离值最小的顶点加入到S中,如此进行下去,直到S中包含了图中所有顶点为止
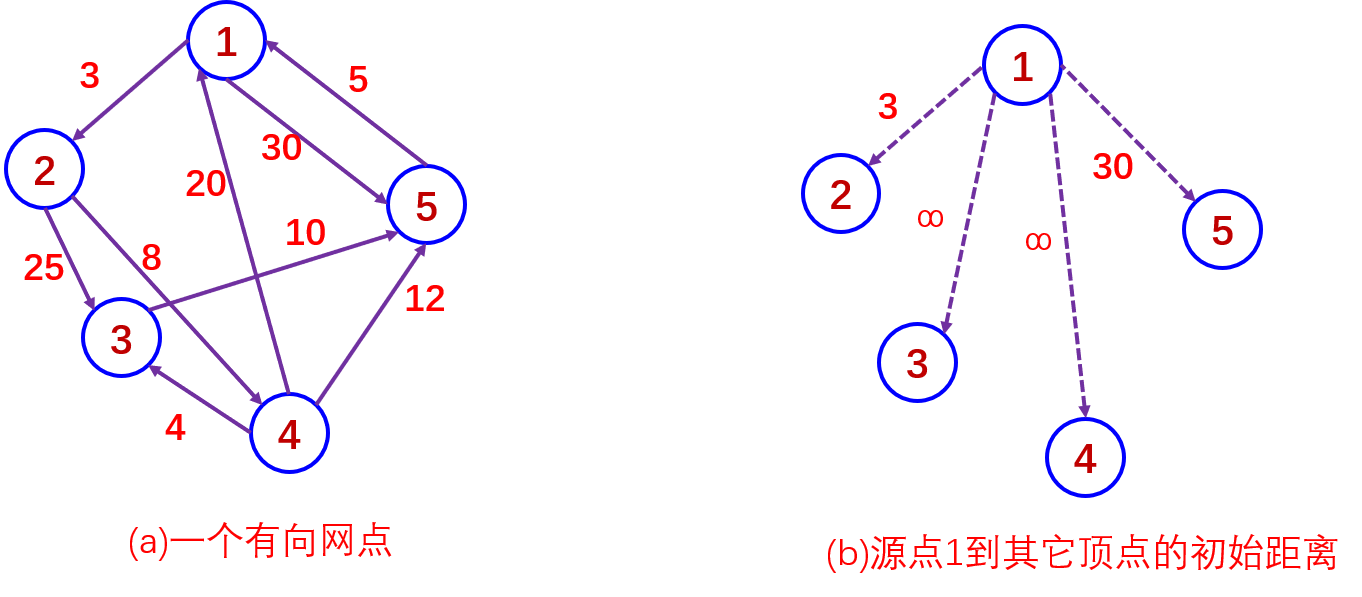
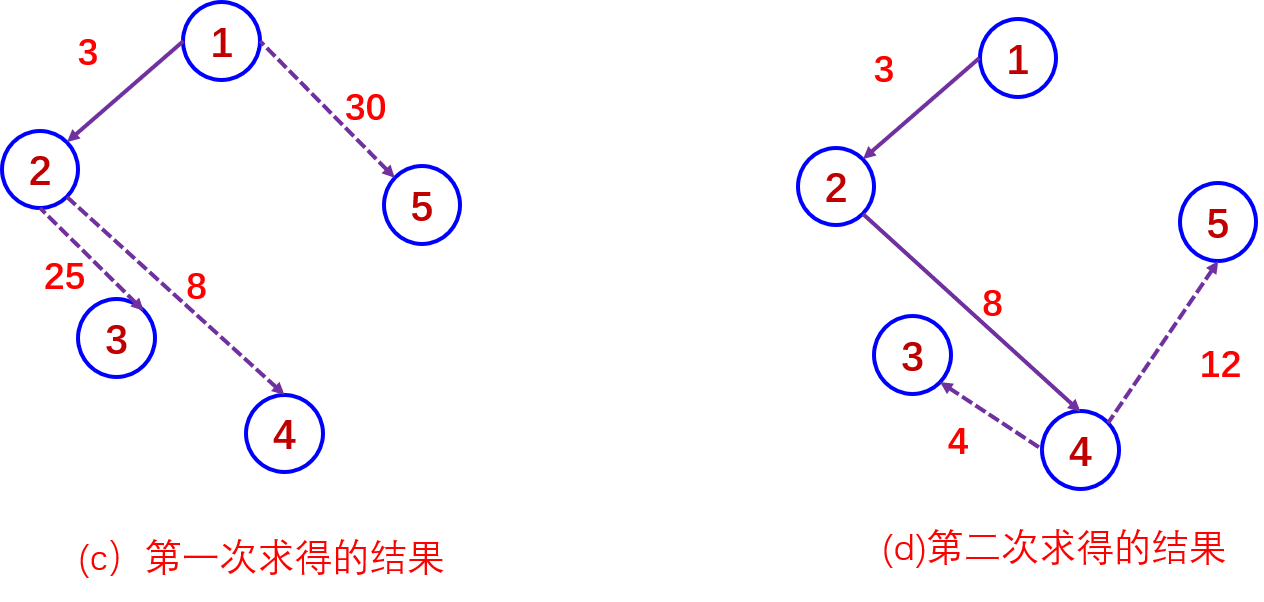
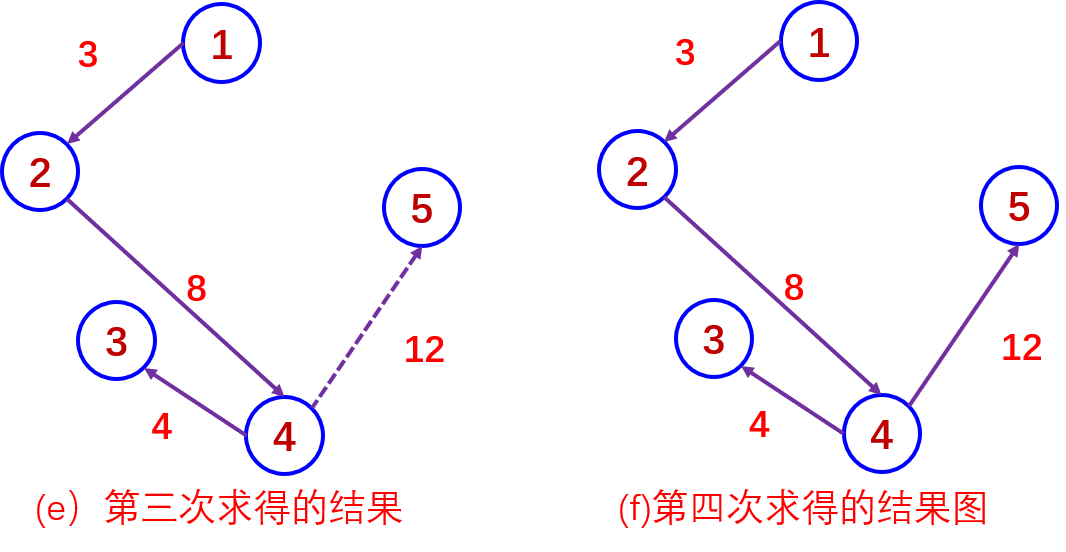
6-27迪杰斯特拉算法求最短路径过程及结果
1. 顶点对之间的最短路径概念
所有顶点对之间的最短路径是指:对于给定的有向网G=(V,E),要对G中任意一对顶点有序对V、W(V≠W),找出V到W的最短距离和W到V的最短距离。
解决此问题的一个有效方法是:轮流以每一个顶点为源点,重复执行迪杰斯特拉算法n次,即可求得每一对顶点之间的最短路径,总的时间复杂度为O(𝑛3 )。
通常我们把计划、施工过程、生产流程、程序流程等都当成一个工程,一个大的工程常常被划分成许多较小的子工程,这些子工程称为活动,这些活动完成时,整个工程也就完成了。例如,计算机专业学生的课程一一 开设可看成是 个工程,每 门课程就是工程中的活动,图6-30给出了若干门所开设的课程,其中有些课程的开设有先后关系,有些则没有先后关系,有先后关系的课程必须按先后关系开设,如开设数据结构课程之前必须先学完程序设计基础及离散数学,而开设离散数学则必须先并行学完高等数学、程序设计基础课程。 ………………..….
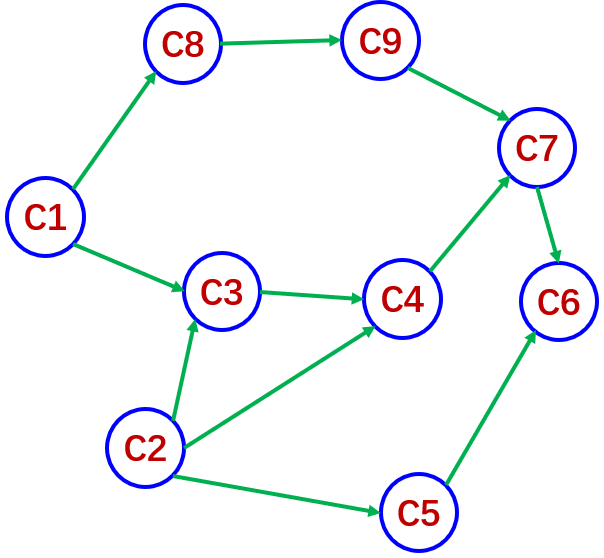
(a)课程开设 |
(b)课程开设优先关系的有向图 |
||||||||||||||||||||||||||||||
|
图6-30学生课程开设工程图 |
|||||||||||||||||||||||||||||||
在图6-30(b)中,我们用一种有向图来表示课程开设,在这种有向
图中,顶点表示活动,有向边表示活动的优先关系,这有向图叫
做顶点表示活动的网络(Actire On Vertices)简称为AOV网。
在AOV网中,<i,j>有向边表示i活动应先于j活动开始,即i活动必须完成后,j活动才可以开始,并称i为j的直接前驱,j为i的直接后继。这种前驱与后继的关系有传递性,此外,任何活动i不能以它自己作为自己的前驱或后继,这叫做反自反性。从前驱和后继的传递性和反自反性来看,AOV网中不能出现有向回路(或称有向环)。在AOV网中如果出现了有向环,则意味着某项活动应以自己作为先决条件,这是不对的,工程将无法进行。对程序流程而言,将出现死循环。
因此,对给定的AOV网,应先判断它是否存在有向环。判断AOV
网是否有有向环的方法是对该AOV网进行拓扑排序,将AOV网中
顶点排列成一个线性有序序列,若该线性序列中包含AOV网全部顶点,则AOV网无环,否则,AOV网中存在有向环,该AOV网所代
表的工程是不可行的。
2. 拓扑排序
下面将介绍怎样实现拓扑排序,实现步骤如下:
(1)在AOV网中选一个入度为0的顶点且输出之;
(2)从AOV网中删除此顶点及该顶点发出来的所有有向边;
(3)重复(1)、(2)两步,直到AOV网中所有顶点都被输出或网中不存在入度为0的顶点从拓扑排序步骤可知,若在第3步中,网中所有顶点都被输出,则表明网中无有向环,拓扑排序成功。若仅输出部分顶点,网中已不存在入度为0的顶点,则表明网中有有向环,拓扑排序不成功。(排序不唯一)

删除入度为零的顶点
|
74.数据结构王道最后8套题第一套第一,8题001页 8.在有向图G的拓扑序列中,若顶点Vi在顶点Vj之前,则下列情形不可能出现的是() |
| A. G中有弧<Vi,Vj> |
| B. G中有一条从Vi到Vj的路径 |
| C. G中没有弧<Vi,Vj> |
| D. G中有一条从Vj到Vi的路径 |
| D |
|
8. D。 (解析]考查拓扑序列的性质。选项D中的情况是不可能出现的,因此若G中有一条Vj到Vi的路径,则要把Vj消去以后才能消去Vi,即在图的拓扑序列中顶点Vj应该在顶点Vi之前。以分析中的示例说明:若有一条Vj到Vi的路径,说明Vj是Vi的前驱,则拓扑排序Vj应该在Vi的前面,显然矛盾。 |
若以带权有向图的顶点代表事件(event)或工程进展状态,用弧表示活动,弧上的权值表示完成该活动所需网 要的时间,则这样的带权有向图称为 AOE 网 (Activity On Edge Network)。
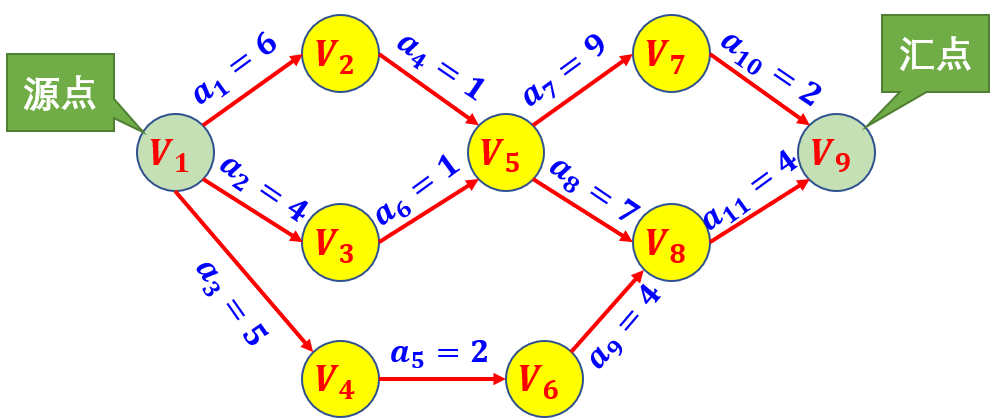
有11项活动(弧),弧上权值表示完成此项活动所需时间。9个事件(顶点)。每个事件表示在在它之前的活动已经完成,在它之后的活动可以开始。
由于整个工程只有一个开始点和一个完成点故在正常情况(无环)下,网中只有一个入度为零的点(称作源点)和一个出度为零的点(称作汇点)。
问题:
①完成整项工程至少需要多少时间?
②哪些活动是影响工程进度的关键?
即:哪些子工程项将影响整个工程的完成期限。
源点 整个工程开始时的那一个顶点
汇点 整个工程结束时的那一个顶点
路径 由源点经由一系列顶点到达汇点所经过的有向边组成(无回路)。注意:路径可以有多条。
源点 整个工程开始时的那一个顶点
汇点 整个工程结束时的那一个顶点
|
74.数据结构王道最后8套题第六套第一,8题041页 8.下列关于AOE网的叙述中,正确的是( )。 |
| A.关键路径上某个活动的时间缩短,整个工程的时间也就必定缩短 |
| B.关键路径上活动的时间延长多少,整个工程的时间也就随之延长多少 |
| C.关键路径上任一关键活动改变后,都必然会影响关键路径的改变 |
| D.若所有的关键路径一同延 长或缩短,则不会引起关键路径的改变 |
| B |
|
8. B。 [解析]考查关键路径的性质。关键路径是从源点到汇点最长的路径,关键路径可能并不唯一,当然各关键路径的路径长度一定是相等的。只有为各关键路径所共有的关键活动,且减少它尚不能改变关键路径的前提下,才可缩短工期,A错误。根据关键路径的定义,关键路径上活动的时间延长多少,整个工程的时间也就必然随之延长多少,B正确。如果是改变所有关键路径上共有的一个关键活动, 则不一定会影响关键路径的改变,C错误。若所有的关键路径同延长,则关键路径不会改变; 但若一同缩短到一定的程度, 则有可能引起关键路径的改变,D错误。 |
路径
由源点经由一系列顶点到达汇点所经过的有向边组成(无回路)。注意:路径可以有多条。
度 度 度 路径长度 组成路径的各有向边上活动所需时间之和
最长路径长度
时间之和最大的路径
最长路径长度
时间之和最大的路径—— 即完成整个工程所需的时间,这是因为所有活动完成之后,即在这条最长路径上的所有活动完成之后,才能完成整个工程
关键路径 将具有最长路径长度的路径称为关键路径
关键活动 不按期完成,则整个工程就不能按期完成的活动
第i个事件最早开始时间Ve(i)
第i个事件V i 最早必须在V i 之前的所有活动都能进行完毕才能开始。所以这个时间等于从源点到它的最长路径长度
活动𝑎𝑘 的最早开始时间e[k]
活动𝑎𝑘 在边<i,j>上。则活动𝑎𝑘的最早开始时间e[k]就等于𝑉𝑖 的最
早开始时间Ve(i)(源点到它的最长路径长度)
活动a k 允许的最迟开始时间l[k]
活动a k 在边<i,j>上。则活动a k 允许的最迟开始时间应该能够确保该活动完成之后,从事件V j 到汇点的工程时间。所以a k 允许的最迟开始时间等于最长路径长度减去V j 到汇点的最长路经长度即V j的最迟开始时间Vl(j),再减去活动a k 所需要的时间,即l[k]=Vl(j)-dur(<i,j>)
松弛时间(即有时间余量)
l[k]-e[k]>0
没有松弛时间(即没有时间余量)
l[k]-e[k]=0,则活动k是关键活动
根据上例分析:AOE网具有下列性质:
(1) 只有在某个顶点代表的事件发生后,从该顶点 出发 的
各条弧所代表的活动才能开始。
(如果事件发生了,意味着相连的活动也可以开始了___含义是什么?)
(2) 只有在 进入 某一顶点的各条弧代表的活动结束后,该
顶点所代表的事件才能发生。
小结:表示一个实际工程的AOE网应该是一个没有回路的带
权有向图。由于整个工程只有一个开始点和一个结束点,因此
AOE网中只有一个入度为0顶点(称为 源点 )和一个出度为0的顶点
(称为 汇点 )。
由于AOE网中的某些活动能够并行地进行,故完成整个工程所必需的时间应为从源点到汇点的最长路径的长度。这里的路径长度是指完成这条路径上各个活动所需的时间之和。从源点到汇点的最长路径称为 关键路径 ( (Critical Path)。关键路径上的活动称为 关键活动

ve[j]表示事件v j 能够最早发生的时间,是从源点到顶点v j 的最长路径的长度。显然事件v j 的最早发生时间 也是从v j j 出发的弧所代表的活动能够最早开始的时间。源点v 0 的最早发生时间ve[0]=0,结束事件v n-1 的最早发生
时间ve[n-1]即为整个工程的完成时间。
vl[j]表示在不推迟整个工期的前提下,事件v j 允许的最晚发生时间。
显然事件v v 的最晚发生时间也是进入v v 的弧所代表的活动最迟应结束的vl[j]表示在不推迟整个工期的前提下,事件v j 允许的最晚发生时间。
显然事件v v j j 的最晚发生时间也是进入v v j j 的弧所代表的活动最迟应结束的时间。为了不延误工期,汇点v n-1 的最晚发生时间vl[n-1]应为工程结束时间,即vl[n-1]=ve[n-1]。
事件v j 的最早发生时间ve[j]为:
\(ve[j]=\begin{cases} 0 若j=0(即vj为源点)\\ Max{ ve[i]+dur(i,j) | <V_i ,V_j >为网中的弧 } \end{cases} \)
注意:ve[i]是vj的一个前驱事件,要在所有前驱事件找出最大的和值。
事件v j 的最晚发生时间vl[j]为:
\(vl[j]=\begin{cases} ve(n-1) 若j=n-1(即 vj为汇点)\\ Min{ vl[k]-dur(j,k) | <V_j ,V_k >为网中的弧 } \end{cases}\)
1)求出所有事件的最早开始时间(<>中从0开始的,如v1是0开始)
Ve[0]=0 (表示事件0最早发生时间是0)
Ve[1]=Max{Ve[0]+dur(<0,1>)}=6 (表示事件1最早发生时间是6)
Ve[2]=Max{Ve[0]+dur(<0,2>)}=4(表示事件2最早发生时间是4)
Ve[3]=Max{Ve[0]+dur(<0,3>)}=5(表示事件3最早发生时间是5)
ve[j]=0 若j=0(即vj为源点)
Max{ ve[i]+dur(i,j) | <v i ,v j >为网中的弧 }
Ve[3] Max{Ve[0] dur(<0,3>)} 5(表示事件3最早发生时间是5)
Ve[4]=Max{Ve[1]+dur(<1,4>),Ve[2]+dur(<2,4>)}=Max{6+1,4+1}=Max{7,5}=7(表示事件4最早发生时间是7)
Ve[5]=Max{Ve[3]+dur(<3,5>)}=5+2=7
Ve[6]=Max{Ve[4]+dur(<4,6>)}=7+9=16
Ve[7]=Max{Ve[4]+dur(<4,7>),Ve[5]+dur(<5,7>)}={7+7,7+4}=14
Ve[8]=Max{Ve[6]+dur(<6,8>),Ve[7]+dur(<7,8>)}={16+2,14+4}=18
Ve[8]是18说明了什么?整个工程至少需要多少天?
2)求出所有事件的最迟开始时间(<>中从0开始的)
Vl[8]=18 (表示事件8最晚发生时间是18,这是也最早发生时间)
Vl[7]=Min{Vl[8]-dur(<7,8>)}=18-4=14 (表示事件7最晚发生时间是14)
\(vl[j]=\begin{cases} ve(n-1) 若j=n-1(即 vj为汇点)\\ Min{ vl[k]-dur(j,k) | <V_j ,V_k >为网中的弧 } \end{cases}\)
Vl[6]=Min{Vl[8]-dur(<6,8>)}=18-2=16 (表示事件6最晚发生时间是16)
Vl[5]=Min{Vl[7]-dur(<5,7>)}=14-4=10 (表示事件5最晚发生时间是10)
Vl[4]=Min{Vl[6]-dur(<4,6>),Vl[7]-dur(<4,7>)}=Min{16-9,14-7}=7
Vl[3]=Min{Vl[5]-dur(<3,5>)}=8
Vl[2]=Min{Vl[4]-dur(<2,4>)}=7-1=6
Vl[1]=Min{Vl[4]-dur(<1,4>)}=7-1=6
Vl[0]=Min{Vl[1]-dur(<0,1>),Vl[2]-dur(<0,1>, Vl[3]-dur(<0,3)}=Min{6-6,6-
4,8-5}=Min{0,2,3}=0
(3)求出所有活动的最早开始时间
e[k]=Ve[i] a k 是在<i,j>上的活动
a 1 <0,1> e[1]=Ve[0]=0 i=0
a 2 <0,2> e[2]=Ve[0]=0 i=0
a 3 <0,3> e[3]=Ve[0]=0 i=0
a 4 <1,4> e[4]=Ve[1]=6 i=1
a 5 <2,4> e[5]=Ve[2]=4 i=2
a 6 <3,5> e[6]=Ve[3]=5 i=3
a 7 <4,6> e[7]=Ve[4]=7 i=4
a 8 <4,7> e[8]=Ve[4]=7 i=4
a 9 <5,7> e[9]=Ve[5]=7 i=5
a 10 <6,8> e[10]=Ve[6]=16 i=6
a 11 <7,8> e[11]=Ve[7]=14 i=7
(4)求出所有活动的最迟开始时间
l[k]=Vl[j]-dur(<i,j>) a k 是活动<i,j>
a 1 <0,1> l[1]=Vl[1]-dur(<0,1>)=6-6=0
a 2 <0,2> l[2]=Vl[2]-dur(<0,2>)=6-4=2
a 3 <0,3> l[3]=Vl[3]-dur(<0,3>)=8-5=3
4 1 ]=]-1 )=7-1= a 4 <1,4> l[4] Vl[4] dur(<1,4>) 7 1 6
a 5 <2,4> l[5]=Vl[4]-dur(<2,4>)=7-1=6
a 6 <3,5> l[6]=Vl[5]-dur(<3,5>)=10-2=8
a 7 <4,6> l[7]=Vl[6]-dur(<4,6>)=16-9=7
a 8 <4,7> l[8]=Vl[7]-dur(<4,7>)=14-7=7
a 9 <5,7> l[9]=Vl[7]-dur(<5,7>)=14-4=10
a 10 <6,8> l[10]=Vl[8]-dur(<6,8>)=18-2=16
a 11 <7,8> l[11]=Vl[8]-dur(<7,8>)=18-4=14
(5)比较每一个活动的最早和最迟开始时间,找出关键活动
l[1]-e[1]=0-0=0 a1
l[4]-e[4]=6-6=0 a4
l[7]-e[7]=7-7=0 a7
I[8]-e[8]=7-7=0 a8
l[10]-e[10]=16-16=0 a10
l[11]-e[11]=14-14=0 a11
(4)关键活动构成关键路径
所以 a 1 a 4 a 7 a 8 a 10 a 11 ,他们组成关键路径
求AOE网中关键路径和关键活动的 算法 步骤为:
1、利用拓扑排序求出AOE网的一个拓扑序列;
2、从拓扑序列的第一个顶点(源点)开始,按拓扑顺序依次计算每个事件的最早发生时间ve[j];
3、从拓扑序列的最后一个顶点(汇点)开始,按逆拓扑顺序依次计算每个事件的最晚发生时vl[j];
4、对每个活动<v i ,v j >,若ve[i]+dur(i,j)=vl[j],则该活动为关键活动,并输出。

评论列表 (0 条评论)