第二章线性表

 2.1 线性表的类型定义

逻辑结构

线性结构→线性表

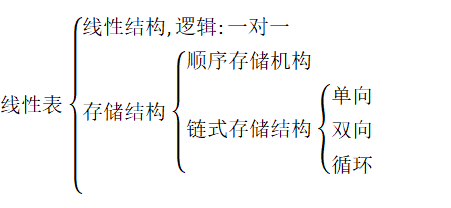
考研→线性表→定义存储→组合操作

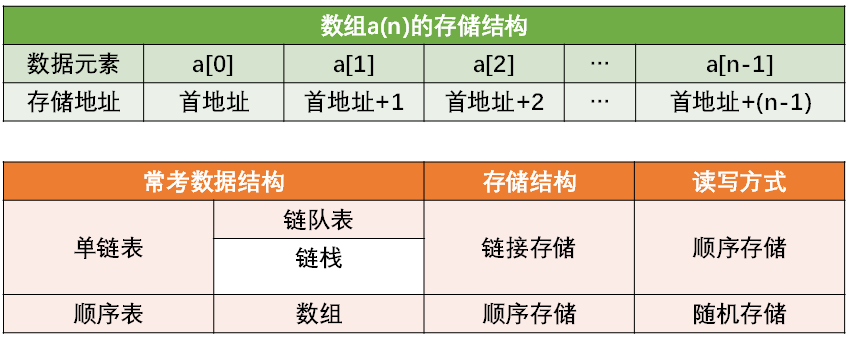
存储结构结构→顺序表(连续的)

线性结构的特点：

在数据元素的非空有限集中

1）有且仅有一个开始结点;

2）有且仅有一个终端结点；

3）除第一个结点外，集合中的每个数据元素均有且只有一个前驱；

4）除最后一个结点外，集合中的每个数据元素均有且只有一个后继。

• 线性序列：线性结构中的所有结点按其关系可以排成一个序列，记为 (a₁,…, a_i, a_i+1,...,a_n )

1）线性表是n(n ≥0)个数据元素的有限序列。

2）线性表是一种最常用且最简单的数据结构。

含有n个数据元素的线性表是一个数据结构：

List = (D,R)

其中：D = {a_i | a_i ∈D₀ ,i=1,2,…n,n≥0}

R = {N}, N = {< a_i-1, a_i > | a_i-1,a_i ∈D 0 , i = 2,3,…n}

D 0 为某个数据对象——数据的子集

• 特性：均匀性，有序性（线性序列关系）

3）线性表的长度及空表

•  线性表中数据元素的个数n（n≥0）定义为线性表的长度当线性表的长度为0 时，称为空表。

2.1 线性表的类型定义

•  当线性表的长度为0 时，称为空表。
• a_i 是第i个数据元素，称i为a_i 在线性表中的位序。

2.2.1 顺序表定义

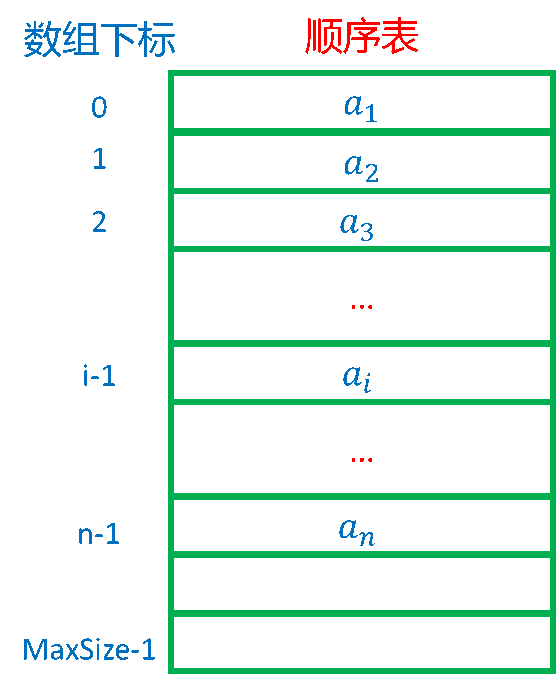
顺序表的示意图

#define MAXSIZE 100

typedef struct{

ElemType *elem

int length;

}Sqlist; //定义顺序表类型

Sqlist L;//定义变量L,L是SqList这种类型的,L是个顺序表

Typedef struct LNode{

ElemType value;

Struct Lnode *next;
}

2.2.2 顺序表的基本操作

1）InitList(&L) 初始化，构造一个空的线性表
2）ListLength(L) 求长度,返回线性表中数据元素个数
3）GetElem(L,i,&e) 取表L中第i个数据元素赋值给e
4）LocateElem(L,e) 按值查找，若表中存在 个或多个值为e的结点，返回第一个找到的数据元素的位序，否则返回一个特殊值。
5）ListInsert(&L,i,e) 在L中第i个位置前插入新的数据元素e，表长加1。
6）ListDelete(&L,i,e) 删除表中第i个数据元素，e返回其值，表长减1。

①插入

bool ListInsert(SqList& L, int i, ElemType e) { if (i<1 || i>L.length + 1) //判断i的范围是否有效 return false; if(L.length >= MaxSize) //当前存储空间已满,不能插入 return false; for (int j = L.length; j >= i; j--) //将第i个元素及之后的元素后移 L.data[j] = L.data[j - 1]; L.data[i - 1] = e; //在位置i处放入e L.length++; //链表长度+1 return true; }

ListInsert(L, 3,  'e') //第三个元素插入一个e

pi=1/(n+1) ∑pi(n-i+1)=n/2

时间复杂度为o(n)

②删除

bool ListDelete(SqList& L, int i, ElemType &e) { //本算法实现删除顺序表L中第i个位置元素 if (i<1 || i>L.length )//判断i的范围是否有效 return false; e=L.data[i-1] //将被删除的元素赋值给e for (int j =i; j< L.length; j++) //将第i个位置之后元素前移 L.data[j-1] = L.data[j]; L.data[i - 1] = e; L.length--; //线性表长度减1 return true; }

ListDelete (L, 3,  e)  //删除第三个元素

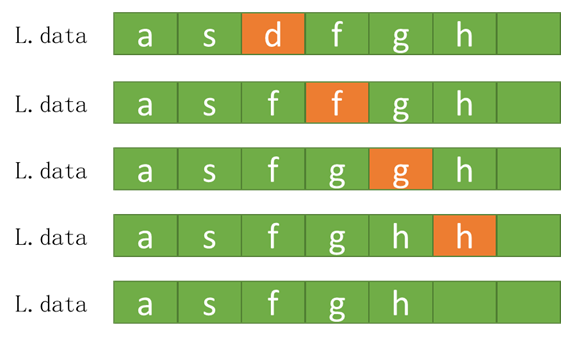
pi=1/(n+1) ∑𝑝𝑖𝑛−𝑖=(𝑛−1)/2

时间复杂度o(n)

③按值查找

查找没有修改值,所以不用引用&

int LocateElem(SqList& L, ElemType e) { //本算法实现查找顺序表中值为e的元素,如果查找成功,返回元素位序,否则返回0 int i for (i=0; i< L.length; i++) if(L.data[i]==e) return i+1; //下标为1的元素等于e,返回其位序i+1 return 0; //如果上面执行完还没返回位序,会执行本步,说明查找失败 }

查找到头没有找到返回0,为什么i+1时从0开始的

2.2.3、存储结构

•   用“物理位置”相邻来表示线性表中数据元素之间的逻辑关系。

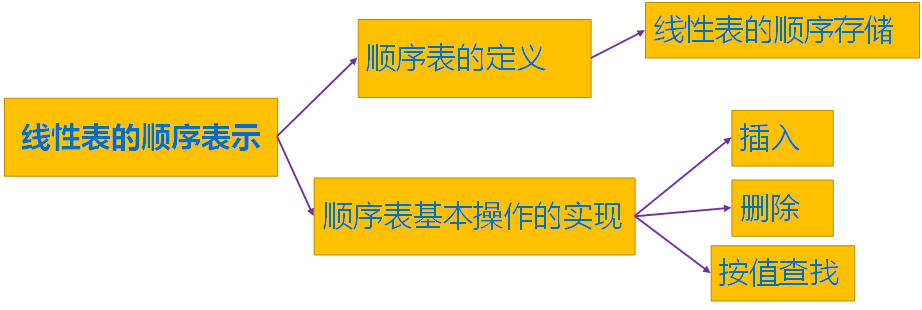
顺序表—线性表的顺序存储结构

•  根据线性表的顺序存储结构的特点，只要确定了存储线性表的起始位置，线性表中任一数据元素都可随机存取，所以，线性表的顺序存储结构是一种随机存取的存储结构

2.3.1 线性表的链式表示和实现

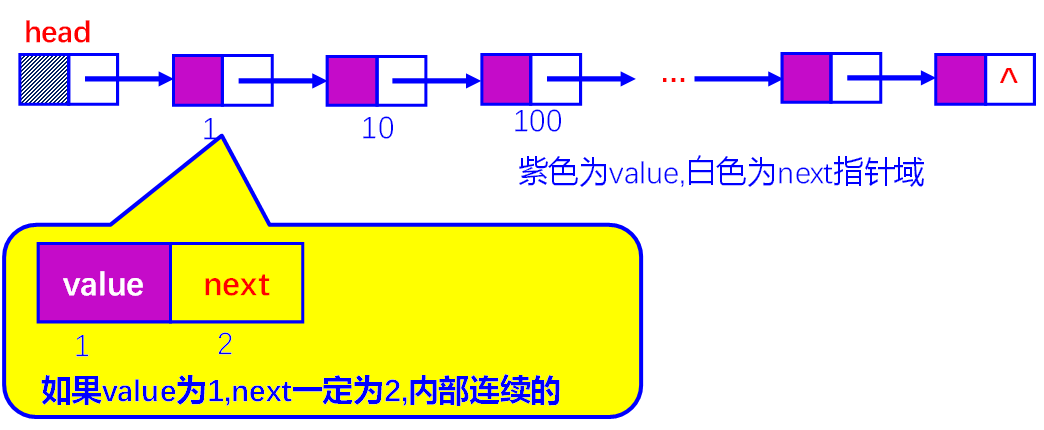
1. 线性链表

• 特点：在内存中用一组任意的存储单元来存储线性表的数据元素，用每个数据元素所带的指针来确定其后继元素的存储位置。这两部分信息组成数据元素的存储映像，称作结点。

结点。

• 结点：数据域 + 指针域（链域）
•  链式存储结构：n个结点链接成一个链表
•  线性链表（单链表）：链表的每个结点只包含一个指针域

对含有n个记录得到表,查找成功时:

顺序查找的平均查找长度:

ASL = P₁+2P₂+…+(n-1)P_𝑛−1+nP_𝑛

假设每个记录的查找概率相等:

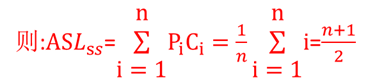
不连续的三个元素10 20 30

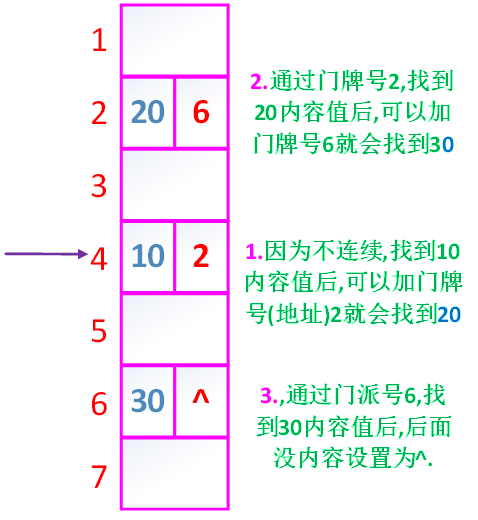
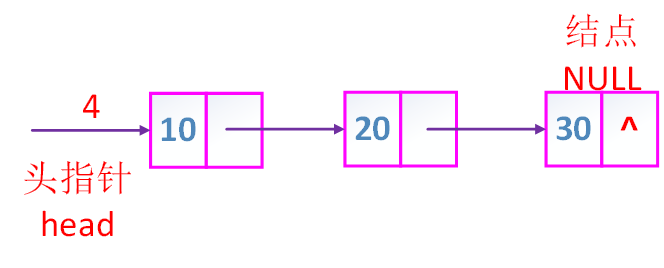
如果插入元素15如图

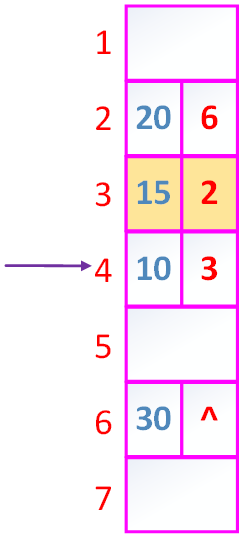
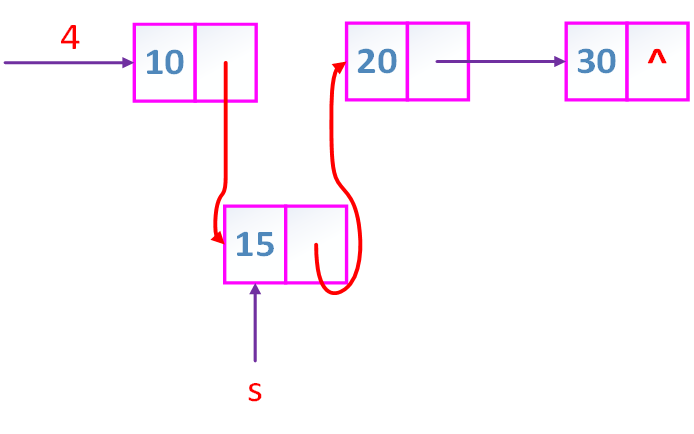
如果删除20

①

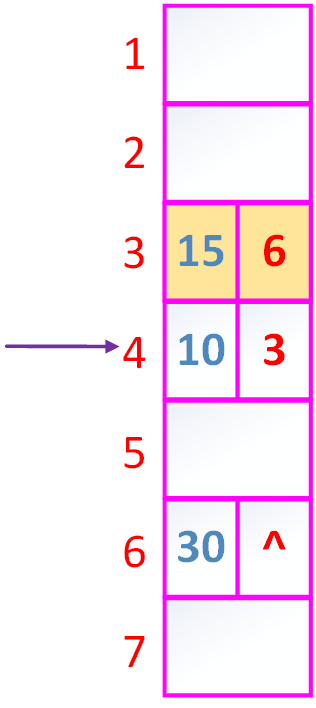
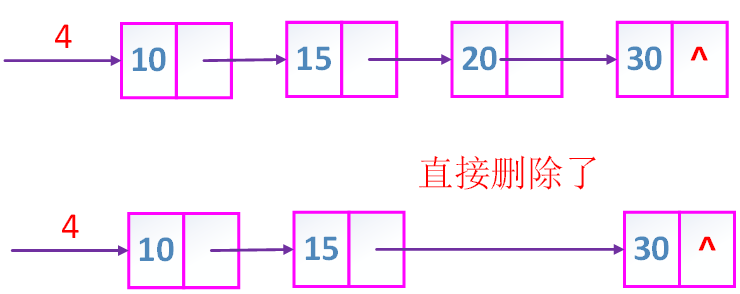
可见删除元素很方便

缺点不能访问挨着的前一个节点,后面节点没有前一个节点的地址(问牌号),只有前一个节点有后一个节点的地址.必须从头开始访问,叫顺序访问.

顺序存储是随机访问,链式存储是顺序访问.

typdef struct node  //声明结点的类型和指向结点的指针类型


{

ElemType data ;// 结点的数据域

struct node  *next;//指向自身的指针域

}      Lnode, *LinkList   //LinkList为指向结构体Lnode的指针类型

2.3.2 单链表结构

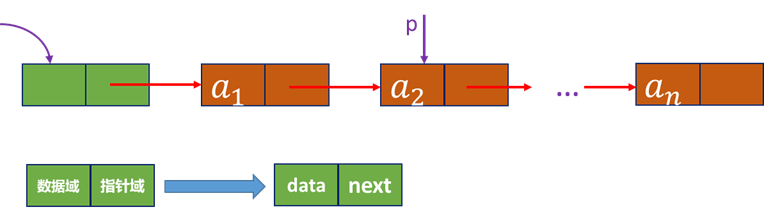
例如，存储学生学号、姓名、成绩的单链表结点类型定义如下:
 

typedef Struct student{
	char num[8]; //数据域
	char name[8]; //数据域
	int score; //数据域
	struct students* next; //指针域
}Lnode, * LinkList;

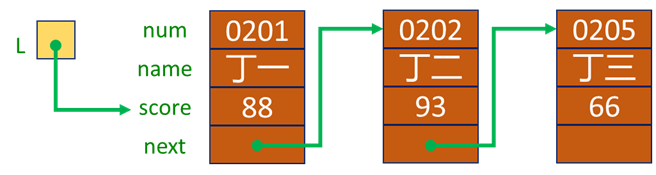
为了统一链表的操作，通常这样定义:

typedef Struct student{
	ElemType data; //数据域
	struct * next; //指针域
}Lnode, * LinkList;

■单链表的初始化(算法2.6)(带头结点的单链表)
■即构造一个如图的空表

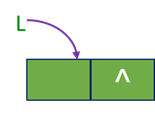
[算法步骤]

(1)生成新结点作头结点，用头指针L指向头结点。
(2)将头结点的指针域置空。
[算法描述]

Status InitList_L(LinkList &L)
{
	L = new Lnode;	
	L->next = NULL;
	return OK;
}

补充单链表的几个常用简单算法

[补充算法1]一判断链表是否为空:
空表:链表中无元素上称为空链表(头指针和头结点仍然在)
[算法思路]判断头结点指针域是否为空
若L是空表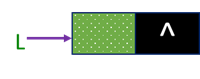  
 

int ListEmpty(LinkList L) //若L为空表,否则返回0
{
	if (L->next) //非空
		return 0;
	else
		return 1;
}

■[补充算法2]一单链表的销毁: 链表销毁后不存在
[算法思路]从头指针开始，依次释放所有结点

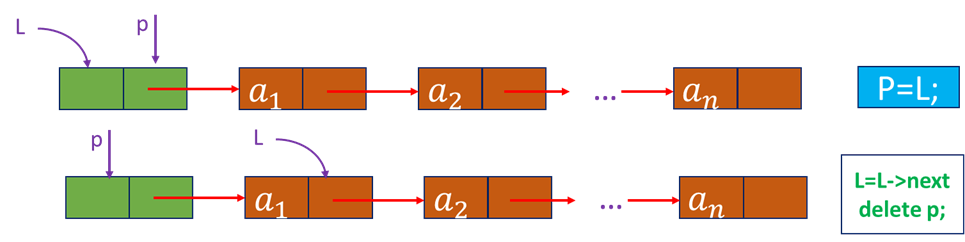
如果用delete前面用new,如果free前面用malloc

Status InitList_L(LinkList& L) //销毁单链表L
{
	L = new Lnode; //或LinkList p;
	while (L)
	{
		p = L;
		L = L->next;
		delete p;
	}	
	return OK;
}

■[补充算法3]--清空链表:
链表仍存在，但链表中无元素,成为空链表(头指针和头结点仍然在)
[算法思路]依次释放所有结点，并将头结点指针域设置为空

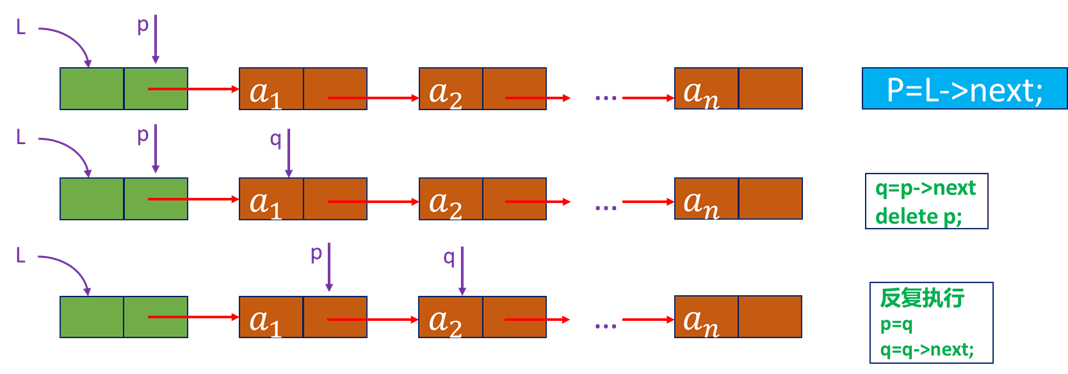
Status InitList_L(LinkList& L) //将L重置为空表
{	
	Lnode *p, *q; //或LinkList p,q;
	p = L->next;
	while (p)	//没到表尾
	{
		q = p->next;
		delete p;
		p = q;
	}
	L->next = NULL;	//头结点指针域为空
	return OK;
}

[补充算法4] -求单链表的表长
[算法思路]从首元结点开始，依次计数所有结点

int ListLength_L(LinkList) //返回L中数据元素的个数
{
	LinkList P;
	p = L->next;	//p指向第一个结点
	i = 0;
	while (p)	//遍历单链表,统计结点数
	{
		i++;
		p = p->next;
	}
	return i;
}

[算法2.7]取值一取单链表中第i个元素的内容
[算法思路]
分别取出表中第3个元素和第15个元素 i=3 i=15  i= -1

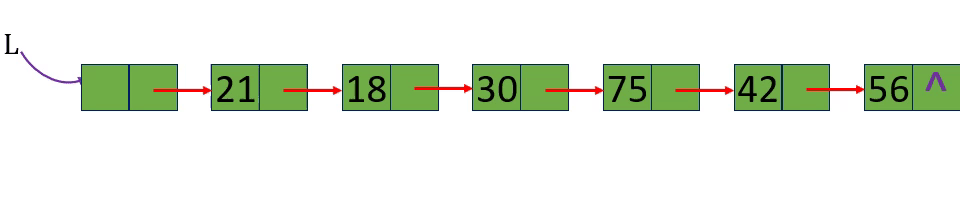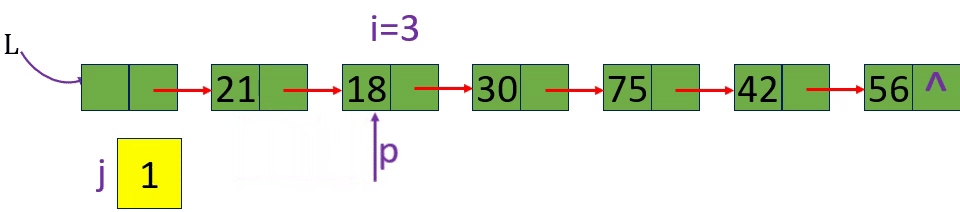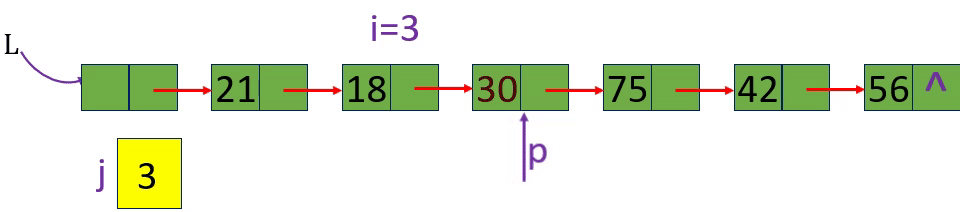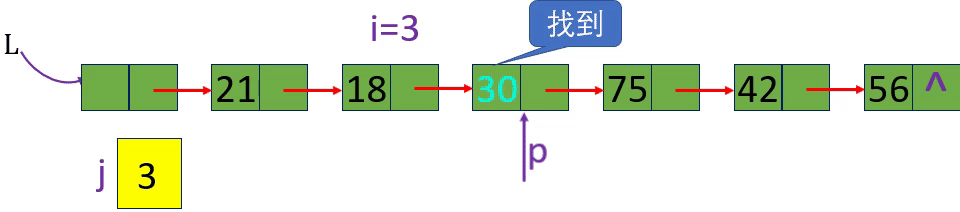
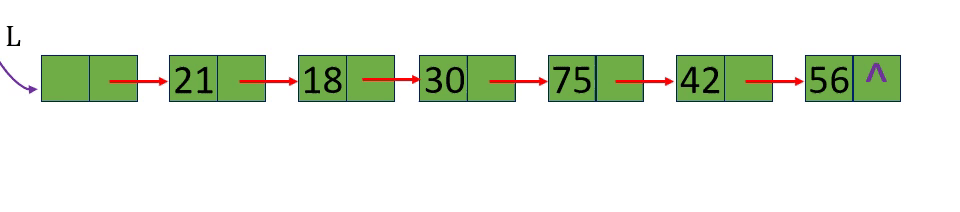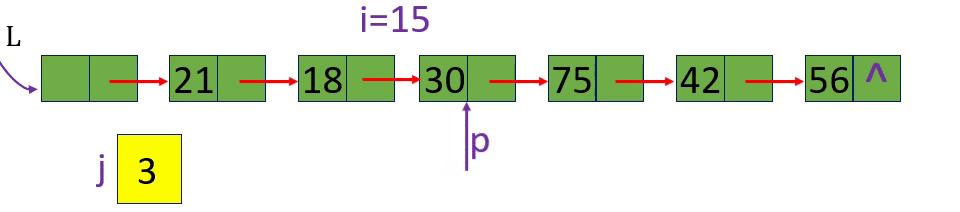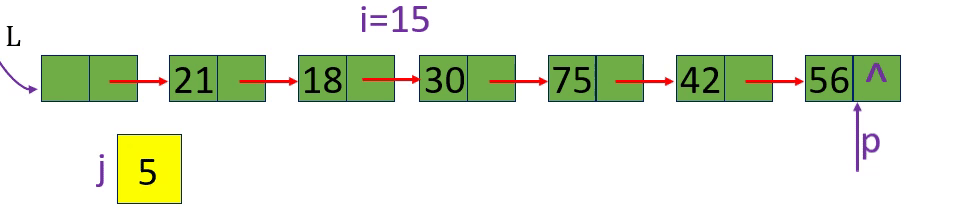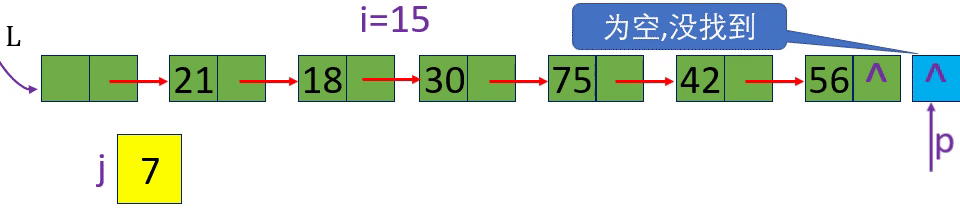
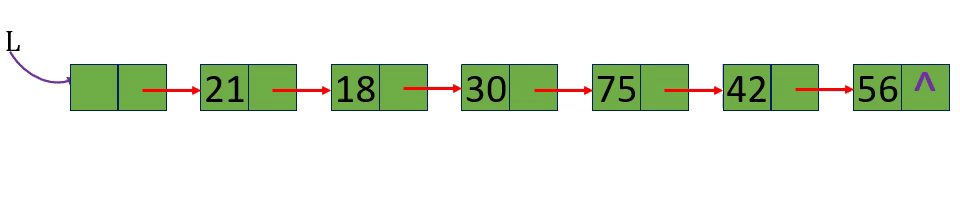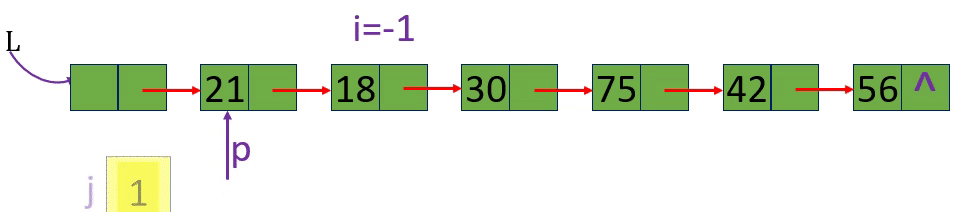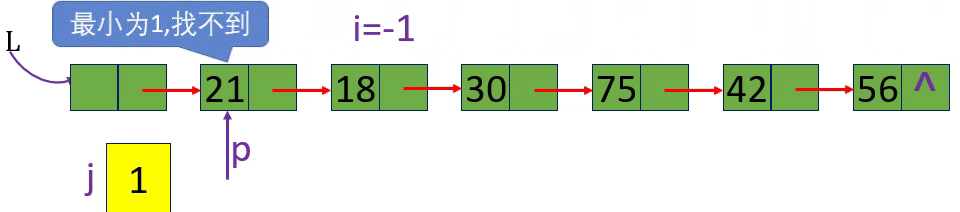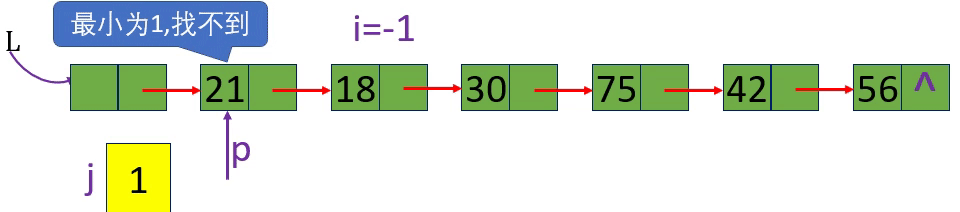
从链表的头指针出发,顺着链域next逐个结点往下搜索,直至搜索到第i个结点为止。因此，链表不是随机存取结构

[算法步骤]

1.从第1个结点(L->next) 顺链扫描，用指针p指向当前扫描到的结点，p初值p= L->next。

2. j做计数器，累计当前扫描过的结点数, j 初值为1.

3.当p指向扫描到的下一结点时，计数器j加1。

4.当j== i时，p所指的结点就是要找的第i个结点。

Staus GetElem L(LinkList L, int i, ElemType& e)
{//获取线性表L中的某个数据元素的内容,通过变量e返回
	p = L->next; j = 1; //初始化
	while (p && j < i) //向后扫描,直到p指向第i个元素或p为空
	{
		p = p->next; ++j;
	}
	if (!p || j > i) return ERROR; //第i个元素不存在
	e = p->data; //取第i个元素
	return OK;
} //GetElem_L

[算法2.8]按值查找一根据指定数据获取该数据所在的位置 (地址)

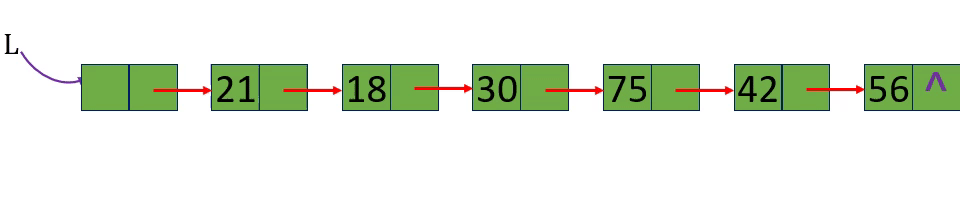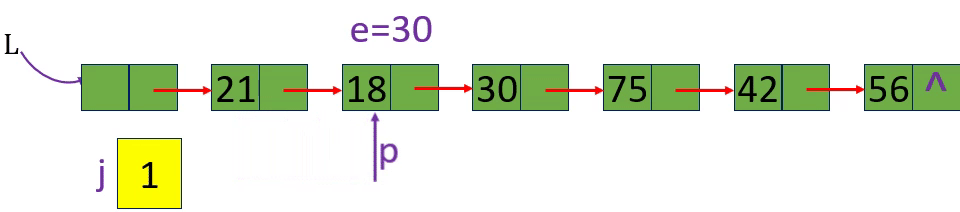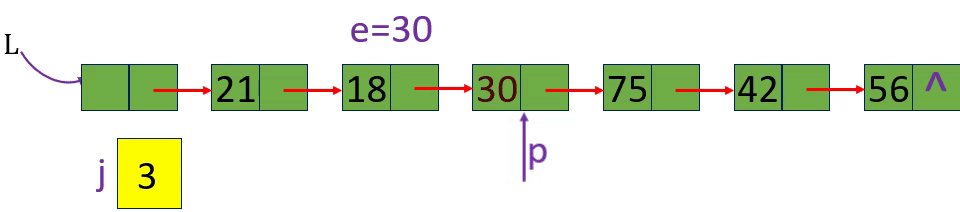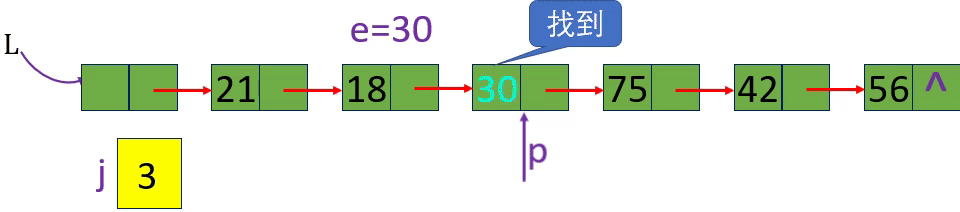
p=L-> next;    p=p-> next;    p->data!=e

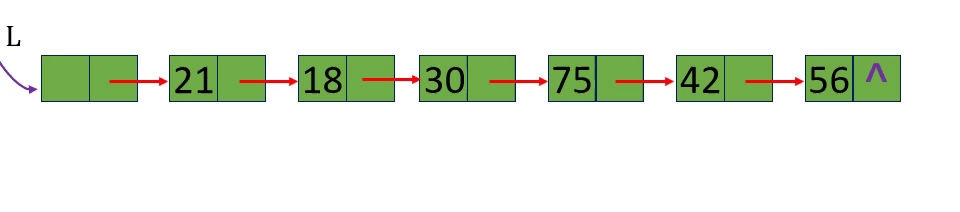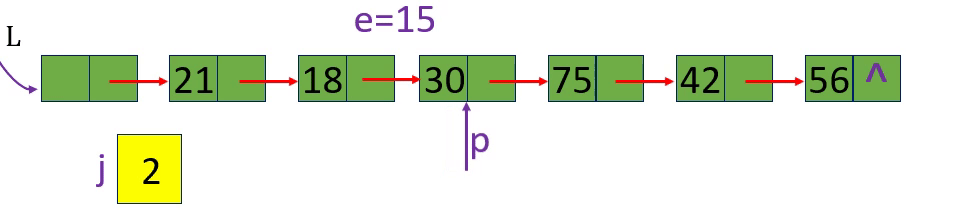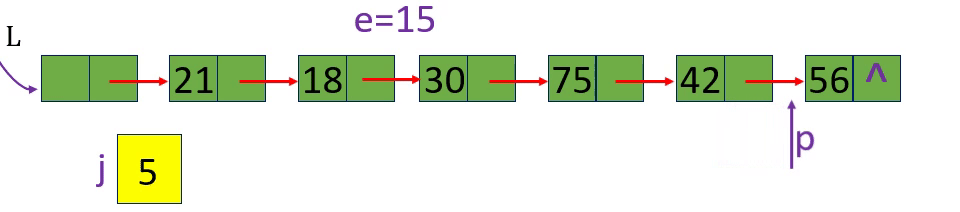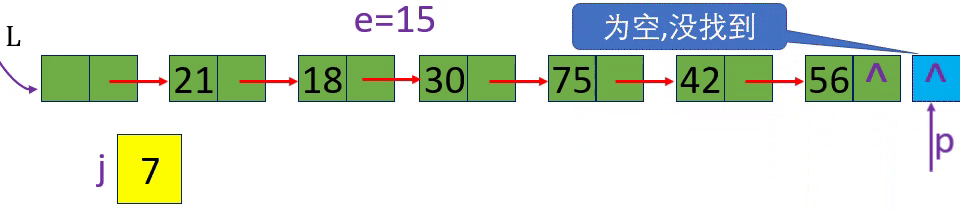
p=L-> next; p=p-> next;  p->data!=e;   p!=NULL或p
未找到返回0
 

//将线性表L中第i个数据元素删除
Status ListDelete_L(LinkList& L, int i, ElemType& e) {
	p = L; j = 0;
	while (p->next && j < i - 1) { p = p->next; ++j; }
	//寻找第i个结点,并令p指向其前驱
	if (!(p->next) || j > i - 1) return ERROR; //删除位置不合理
	q = p->next; //临时保存被删结点的地址以备释放
	p->next = q->next; //改变删除结点前驱结点的指针域
	e = q->data; //保存删除结点的数据域
	delete q; //释放删除结点的空间
	return OK;
}//ListDelete_L

2.3.3 单链表操作
1.创建链表

struct node *p1, *p2,*p3;
	p1=new node;
	p1->data=a1
	p2=new node;
	p2->data=p2
	p1->next=p2
	p2->next=p1
//但是创建很多时用for循环.

创建链表两种方式
①栈式创建(前插:p2->next=p1)
②队式创建(后插:p1->next=p2)

2.链表查询\(\left\{\begin{matrix} {序号}\\{数据} \end{matrix}\right.\)

作为链表,头结点不能乱动,不然乱了,

if(p0->data==a3)
//判断p0的数据是否等于a3的数据
while (p0->data!=a3)
p0=p0->next

3.链表的插入
①头插法

void CreateList_H(LinkList& L, int n)
{
	L = new LNode;
	L->next = NULL; //先建立一个带头结点的单链表
	for (i = n; i > 0; i++)
	{
		p = new LNode; //生成结点
		cin >> p->data; //输入元素值
		p->next = L->next; //插入到表头
		L->next = p;
	}
}//CreateList_hH

②尾插法
[算法2.12]建立单链表:尾插法元素插入在链表尾部，也叫尾插法
1.从一个空表L开始,将新结点逐个插入到链表的尾部，尾指针r指向链表的尾结点。
2.初始时，r同L均指向头结点。每读入一个数据元素则申请一个新结点,将新结点插入到尾结点后，r指向新结点。

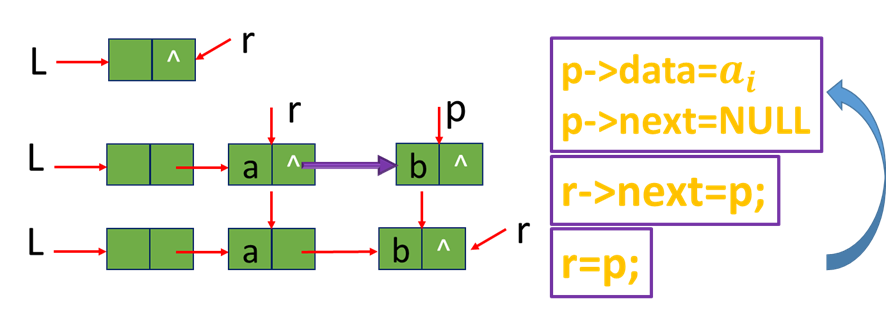
[算法描述]

//正位序输入n个元素的值， 建立带表头结点的单链衣L
void CreateList_R(LinkList& L, int n) {
	L = new LNode;
	L->next = NULL;
	r = L; //尾指针r指向头结点
	for (i = 0; i<n; ++i) {
		p = new LNode; cin >> p->data; //生成新结点，输入元素值
		p->next = NULL;
		r->next = p; //插入到表尾
		r = p;  //r指向新的尾结点
	}//CreateList R
	//算法的时间复杂度是: O(n)

4.查找

//1.按序号查找
	LNode* GetE1em(LinkList L, int i) {
		int j = 1;
		LNode* p = L ->next;
		if (i == 0)
			return L;
		if (i < 1)
			return NULL; _
			while (p && j < i) {
				p = p->next;
				j++;
			}
		return p;
	}

//2.按值查找
	LNode *LocateElem(LinkList L, ElemType e) {
		LNode* p = L->next;
			while (p != NULL && p->data != e)
				p = p->next;
			return p;
}

5.链表的删除

 
 
while(p->next->data!=40)
                        p=p->next              两步循环找40结点
 
为什么是q->next->next,因为20节点为q->next所以30结点为q->next->next
如：
a、请将结点b从链表中删除。
b、请将结点d从链表中删除。
c、请将结点a从链表中删除并让head重新指向链表的第一个结点。
 
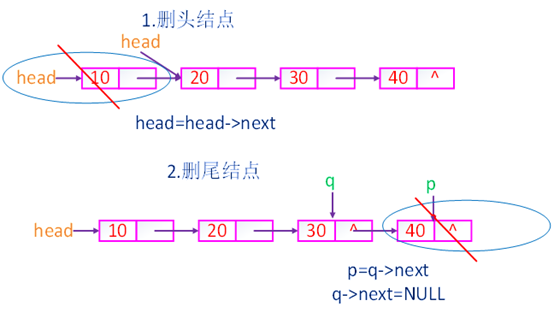
注:如果删头,头直接下移,要删除中间和尾部地址要知道删的结点前面结点的地址
删完之后要释放的.

2.3.4.循环链表

循环列表每个结点都能找到

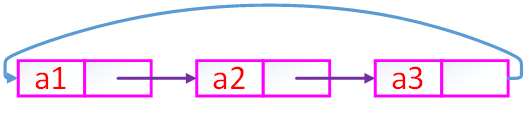
双向链表

既能找前驱又能找后继,缺点浪费空间

1）循环链表一是一种首尾相接的链表。
循环链表最后一个结点的next指针不为0(NULL)，而是指向了表头结点。在循环链表中没有NULL为简化操作，在循环表中往往加入表头结点。
 特点：循环链表中，从任一结点出都可访问到表中所有须从头指开始，否则无法访问到该节点之前的其他结点.
循环链表一单链表不同的是链表中表尾结点的指针域不是NULL，而是链表、结点的指针H（链表指针）
 

注意:

由于循环链表中没有NULL指针,故涉及遍历操作时，其终止条件就不再像非循环链表那样判断p或p- >next是否为空，而是判断它们是否等于头指针。

循环条件:

p!=NULL  ->  p!=L

p-> next!=NULL  ->  p->next!=L

单链表  单循环链表

\(头指针表示 单循环链表\begin{cases}找𝑎_1 的时间复杂度: \color{red}{0(1)}\\ 找𝑎_𝑛 的时间复杂度: \color{red}{0(n)}\\ \end{cases} \)不方便

注意:表的操作常常是在表的首尾位置上进行。

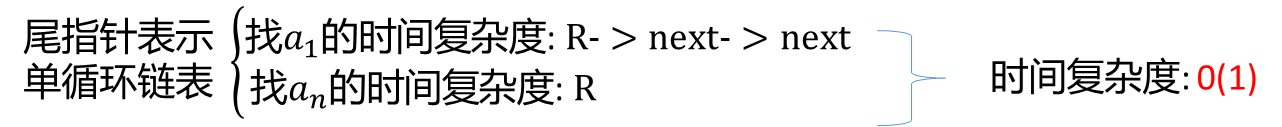
带尾指针循环链表的合并(将Tb合并在Ta之后)

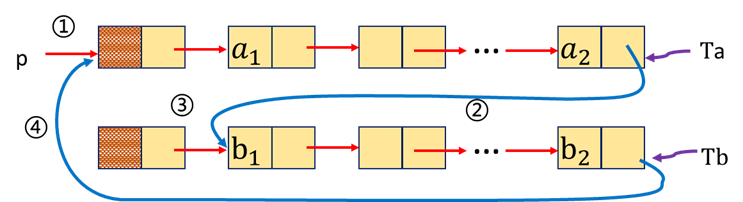
分析有哪些操作?

● p存表头结点 ●Tb表头连接到Ta表尾 ●释放Tb表头结点 ●修改指针

p=Ta-> next;   Ta->next= Tb->next-> next ;   delete Tb-> next;   Tb->next=p;

带尾指针循环链表的合并
[算法描述]

LinkList Connect(LinkList Ta, LinkList Tb) {
	//假设Ta、Tb都是非空的单循环链表
	p = Ta->next; //①p存表头结点
	Ta->next = Tb->next->next; //②Tb表头连结Ta表尾
	delete Tb - > next; //③释放Tb表头结点
	Tb->next = p; . //④修改指针
	return Tb;
}

2.3.4. 双向链表(DoublyLinkedList)
 

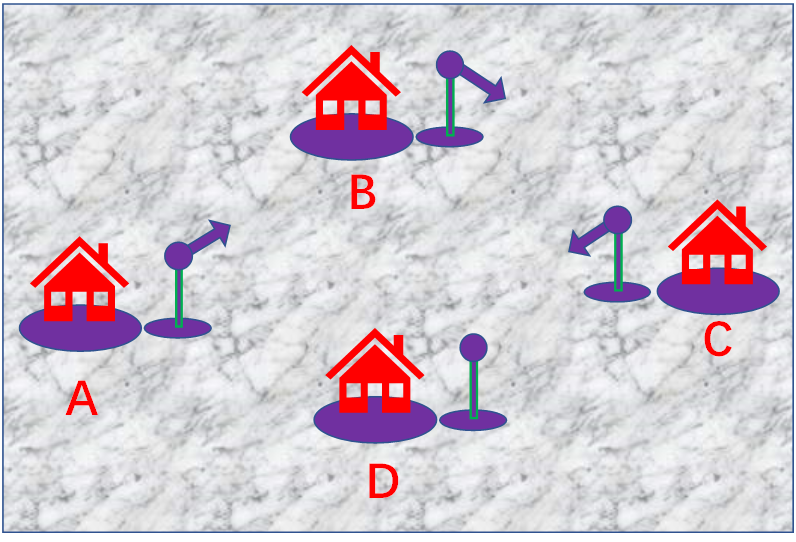
每个旁边插个方向指示标,让它指向前面一个房子,

就变成双链表

到双向链表是指在前驱和后继方向都能游历（遍历）的线性链表。

1)双向链表的结点结构：

前驱方向⟵(a)结点结构⟶后继方向

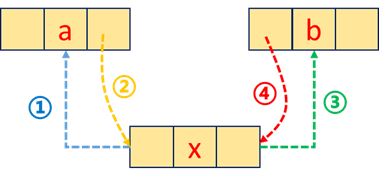
1.S-> prior=p-> prior;

2.p-> prior-> next=S;

3.S-> next= p;

4.p-> prior=S;