机器学习3

1.欠拟合和过拟合

一、欠拟合（Underfitting）
模型在训练数据上不能获得很好的拟合，并且在测试数据集上也不能很好的拟合数据，这种现象称为欠拟合，即高偏差（high bias）。(模型过于简单)

原因：模型不够复杂、拟合函数的能力不足，学习到的有用特征太少，导致拟合的函数无法满足训练集。

二、过拟合（Overfitting）
模型在训练数据上能够获得很好的拟合，但是在测试数据集上却不能很好的拟合数据，这种现象称为过拟合，即高方差（high variance）。(模型过于复杂，泛化能力差)

1. 对于数据集来说，模型过于复杂、拟合能力过强，学习了训练数据中的噪声和训练样例中没有代表性的特征，导致模型学习到的特征数过多。
2. 训练数据不足，即训练数据无法对整个数据的分布进行估计。

.交叉验证（cross-validation）

先解释一下bias和variance的概念。模型的Error = Bias + Variance，Error反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。

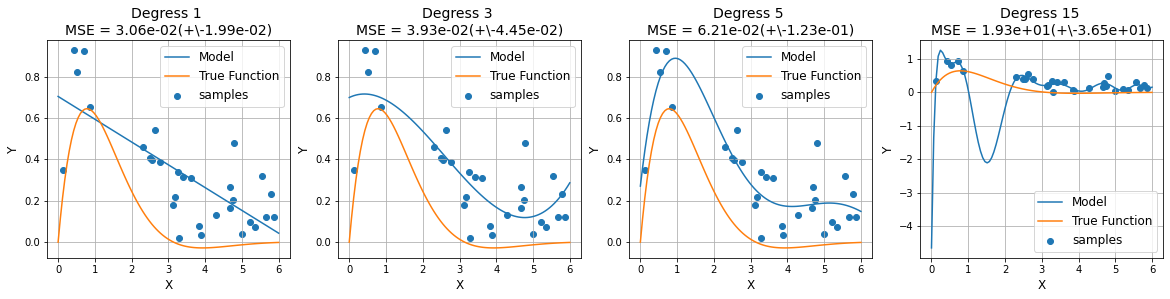
在缺少有效预防欠拟合和过拟合措施的情况下，随着模型拟合能力的增强，错误率在训练集上逐渐减小，而在验证集上先减小后增大；当两者的误差率都较大时，处于欠拟合（high bias, low variance）；当验证集误差率达到最低点时，说明拟合效果最好，由最低点增大时，处于过拟合（high variance, low bias）。下图的横坐标用拟合函数多项式的阶数笼统地表征模型拟合能力：
 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score


def true_fun(x):
    return 2 * np.exp(-x) * np.sin(x)


def data_samples():
    # 从真是函数采样数据，并添加噪声。模拟真实数据
    np.random.seed(0) # 随机种子
    n_samples = 30
    X = np.sort(0 + np.random.rand(n_samples) * (6-0)) # 【0，6】区间分布采样
    y = true_fun(X) + np.random.random(n_samples) * 0.5 # 添加噪声
    return X,y


def model_trian(X, y):
    # 模型训练和测试，采用多项式回归，最高阶次【1，3，5，15】
    degress = [1, 3, 5, 15]
    plt.figure(figsize=(20,4))
    for i in range(len(degress)):
        plt.subplot(1,len(degress), i+1)
        polynomial_features = PolynomialFeatures(degress[i], include_bias=False) # 多项式数据特征处理
        linear_regression = LinearRegression() # 先行回归模型
        pipeline = Pipeline([("polynomial_features", polynomial_features), ("linear_regression", linear_regression)])
        pipeline.fit(X[:, np.newaxis], y) # [:, np.newaxis] 取一行
        scores = cross_val_score(pipeline, X[:, np.newaxis], y, scoring='neg_mean_squared_error', cv=10) # 10次交叉验证
        # print(scores)
        # 绘制图像
        X_test = np.linspace(0, 6, 100)
        plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label='Model')
        plt.plot(X_test, true_fun(X_test), label="True Function")
        plt.scatter(X, y, label="samples")
        plt.legend(loc="best", fontsize=12)
        plt.xlabel("X", fontsize=12)
        plt.ylabel("Y", fontsize=12)
        plt.grid()
        plt.title("Degress {} \nMSE = {:.2e}(+\-{:.2e})".format(degress[i], -scores.mean(), scores.std()), fontsize=14)
        
plt.show()
    

X, y = data_samples()
model_trian(X, y)

2.留出法(hold-out)
直接将数据集D划分为两个互斥的集合，其中一个集合作为训练集S，另外一个作为测试集T，

即D=S∪T,S∩T=∅.

在S上训练出模型后，用T来评估其测试误差，作为对泛化误差的评估
需要注意的问题：
1.训练/测试集的划分要尽可能的保持数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响
2.在给定训练/测试集的样本比例后，仍然存在多种划分方式对初始数据集D进行划分，可能会对模型评估的结果产生影响。因此，单次使用留出法得到的结果往往不够稳定可靠，在使用留出法时，一般采用若干次随机划分、重复进行实验评估后取得平均值作为留出法的评估结果
3.此外。我们希望评估的是用D训练出的模型的性能，但是留出法需划分训练/测试集，这就会导致一个窘境：若另训练集S包含大多数的样本，则训练出的模型可能更接近于D训练出的模型，但是由于T比较小，评估结果可能不够稳定准确；若另测试集T包含多一些样本，则训练集S与D的差别更大，被评估的模型与用D训练出的模型相比可能就会有较大的误差，从而降低了评估结果的保真性（fidelity）。因此，常见的做法是：将大约2/3~4/5的样本用于训练，剩余样本作为测试
4.一般而言。测试集至少应包含30个样例
实例：数据集包含1000个样本，其中500个正例、500个反例，将其划分为包含70%样本的训练集和30%的样本测试集用于留出法评估，试估算有多少划分方式
{C_500150}2
 

2.1 API

参数解读：train_test_split (*arrays，test_size, train_size, rondom_state=None, shuffle=True, stratify=None)

arrays：特征数据和标签数据（array，list，dataframe等类型），要求所有数据长度相同。
test_size / train_size: 测试集/训练集的大小，若输入小数表示比例，若输入整数表示数据个数。
rondom_state：随机种子（一个整数），其实就是一个划分标记，对于同一个数据集，如果- rondom_state相同，则划分结果也相同。
shuffle：是否打乱数据的顺序，再划分，默认True。

stratify : none或者array/series类型的数据，表示按这列进行分层采样。
标准化:StandardScaler，格式: sklearn.preprocessing.StandardScaler(copy=True, with_mean=True, with_ std=True)

import numpy as np
import pandas as pd

wdbc = pd.read_csv("http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data", header=None) # 在线加载
wdbc.head()

	0	1	2	3	4	5	6	7	8	9	...	22	23	24	25	26	27	28	29	30	31
0	842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678

5 rows × 32 columns

from sklearn.preprocessing import LabelEncoder, StandardScaler # 类别标签编码，标准化处理
X, y = wdbc.loc[:, 2:].values, wdbc.loc[:, 1] # 提取特征数据和样本标签集
X = StandardScaler().fit_transform(X)  # 对样本特征数据进行标准化
lab_en = LabelEncoder() # 对目标值进行编码，创建对象
y = lab_en.fit_transform(y) # 拟合和转换
lab_en.classes_, lab_en.transform(["B", "M"])

(array(['B', 'M'], dtype=object), array([0, 1]))
 

# 降噪，降维，可视化
from sklearn.decomposition import PCA # 主成分分析
pca = PCA(n_components=6).fit(X) # 选取6个主成分,30维降到6维
evr = pca.explained_variance_ratio_ # 解释方差比，即各个主成分的贡献率
print("各主成分贡献率", evr, '\n累计贡献率', np.cumsum(evr))

各主成分贡献率 [0.44272026 0.18971182 0.09393163 0.06602135 0.05495768 0.04024522] 
累计贡献率 [0.44272026 0.63243208 0.72636371 0.79238506 0.84734274 0.88758796]

X_pca = pca.transform(X) # 转换获得各个主成分数据
print(X_pca[:5, :])

[[ 9.19283683  1.94858307 -1.12316617  3.63373086 -1.19511037  1.41142498]
 [ 2.3878018  -3.76817174 -0.52929269  1.11826385  0.62177494  0.02865647]
 [ 5.73389628 -1.0751738  -0.55174759  0.91208274 -0.1770856   0.54145141]
 [ 7.1229532  10.27558912 -3.23278955  0.15254701 -2.96087849  3.05342206]
 [ 3.93530207 -1.94807157  1.38976673  2.94063936  0.5467475  -1.22649487]]

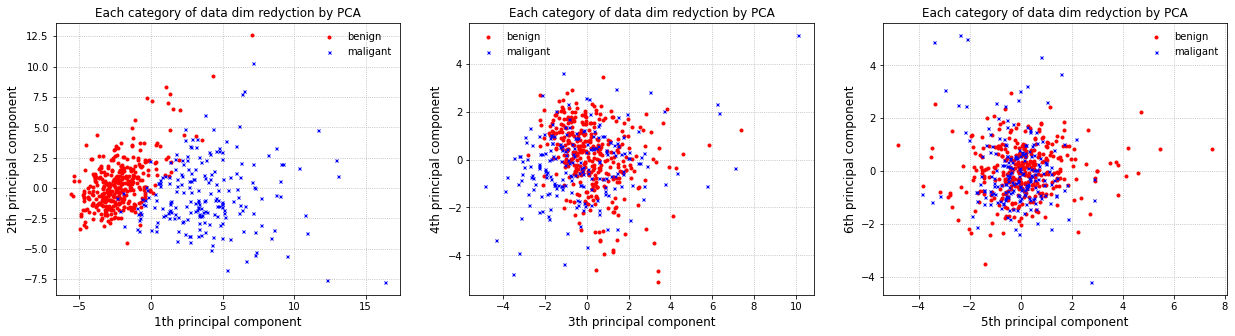
import matplotlib.pyplot as plt
plt.figure(figsize=(21, 5))
X_b, X_m = X_pca[y==0], X_pca[y==1] # 把降维后的数据安类别分类提取
for i in range(3):
    plt.subplot(131 + i)
    plt.plot(X_b[:, i * 2], X_b[:, i * 2 + 1], 'ro', markersize=3, label='benign')
    plt.plot(X_m[:, i * 2], X_m[:, i * 2 + 1], 'bx', markersize=3, label='maligant')
    plt.legend(frameon=False)
    plt.grid(ls=":")
    plt.xlabel(str(2 * i +1) + "th principal component", fontsize=12)
    plt.ylabel(str(2 * i +2) + "th principal component", fontsize=12)
    plt.title("Each category of data dim redyction by PCA", fontsize=12)
plt.show()

• 数据集做完之后然后进行采样，划分，训练

from sklearn.model_selection import train_test_split # 划分数据集
from sklearn.linear_model import LogisticRegression # 逻辑回归
from sklearn.metrics import classification_report, accuracy_score # 分类报告， 正确率
acc_test_score, acc_train_score = [], [] # 每次随机划分训练和测试评分
for i in range(50):
    X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.25, random_state=i, shuffle=True, stratify=y)
    log_reg = LogisticRegression() # 未掌握远离之前，所有参数默认
    log_reg.fit(X_train, y_train) # 采用训练集训练模型
    y_test_pred = log_reg.predict(X_test) # 模型训练完毕后，对测试样本预测
    acc_test_score.append(accuracy_score(y_test, y_test_pred))
    acc_train_score.append(accuracy_score(y_train, log_reg.predict(X_train)))

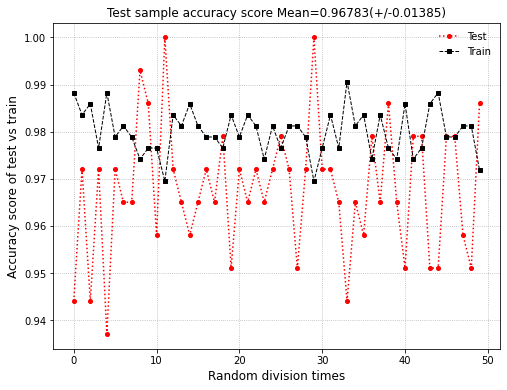
plt.figure(figsize=(8, 6))
plt.plot(acc_test_score, 'ro:', lw=1.5, markersize=4, label='Test')
plt.plot(acc_train_score, 'ks--', lw=1, markersize=4, label='Train')
plt.legend(frameon=False)
plt.grid(ls=":")
plt.xlabel("Random division times", fontsize=12)
plt.ylabel("Accuracy score of test vs train", fontsize=12)
plt.title("Test sample accuracy score Mean=%.5f(+/-%.5f)" % (np.mean(acc_test_score), np.std(acc_test_score)), fontsize=12)
plt.show()

• Pipeline

Pipeline 可以把多个评估器链接成一个。这个是很有用的，因为处理数据的步骤一般都是固定的，例如特征选择、标准化和分类。

Pipeline 主要有两个目的:

便捷性和封装性

你只要对数据调用  ``fit``和  ``predict``一次来适配所有的一系列评估器。

联合的参数选择

你可以一次 :ref: `grid search <grid_search>`管道中所有评估器的参数。

安全性

训练转换器和预测器使用的是相同样本，管道有助于防止来自测试数据的统计数据泄露到交叉验证的训练模型中。

管道中的所有评估器，除了最后一个评估器，管道的所有评估器必须是转换器。 (例如，必须有 transform 方法). 最后一个评估器的类型不限（转换器、分类器等等）

from sklearn.pipeline import Pipeline, make_pipeline

X, y = wdbc.loc[:, 2:].values, wdbc.loc[:, 1] # 提取特征数据和样本标签集
lab_en = LabelEncoder().fit_transform(y) # 对目标值进行编码


pipe_lr = make_pipeline(StandardScaler(),  # 标准化，数据保留相同的数量级
                        PCA(n_components=10),# 主成分分析，降维
                       LogisticRegression())  # 具体模型:逻辑回归
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0, shuffle=True, stratify=y)
pipe_lr.fit(X_train, y_train)
print("Test Accuracy is %.5f" % pipe_lr.score(X_test, y_test))

Test Accuracy is 0.96503