第一章:绪论(数据结构)
不同结构操作效率是不一样的.
顺序存储结构也叫连续存储结构
存取方式→随机存取、串行(顺序)存取、直接存取
存取方式→顺序、链式、索引、散列
存取 随串直
李明到存钱机取钱,取了100元,去小吃摊买了1瓶矿泉水和1窜羊肉串和1个芝麻饼
存储 顺链索散
然后去商店买了老陈醋,正准备回家是,发现孙子把自行车链子用索锁住了,他气愤冲了过去扇了孙子一巴掌
定义/特点
抽象数据类型 ADT\(\begin{equation}\begin{cases} 存储+操作, \\ 描素规则 \\ \end{cases}\end{equation}\)
ADT 类型名
{
实现每一个操作
}
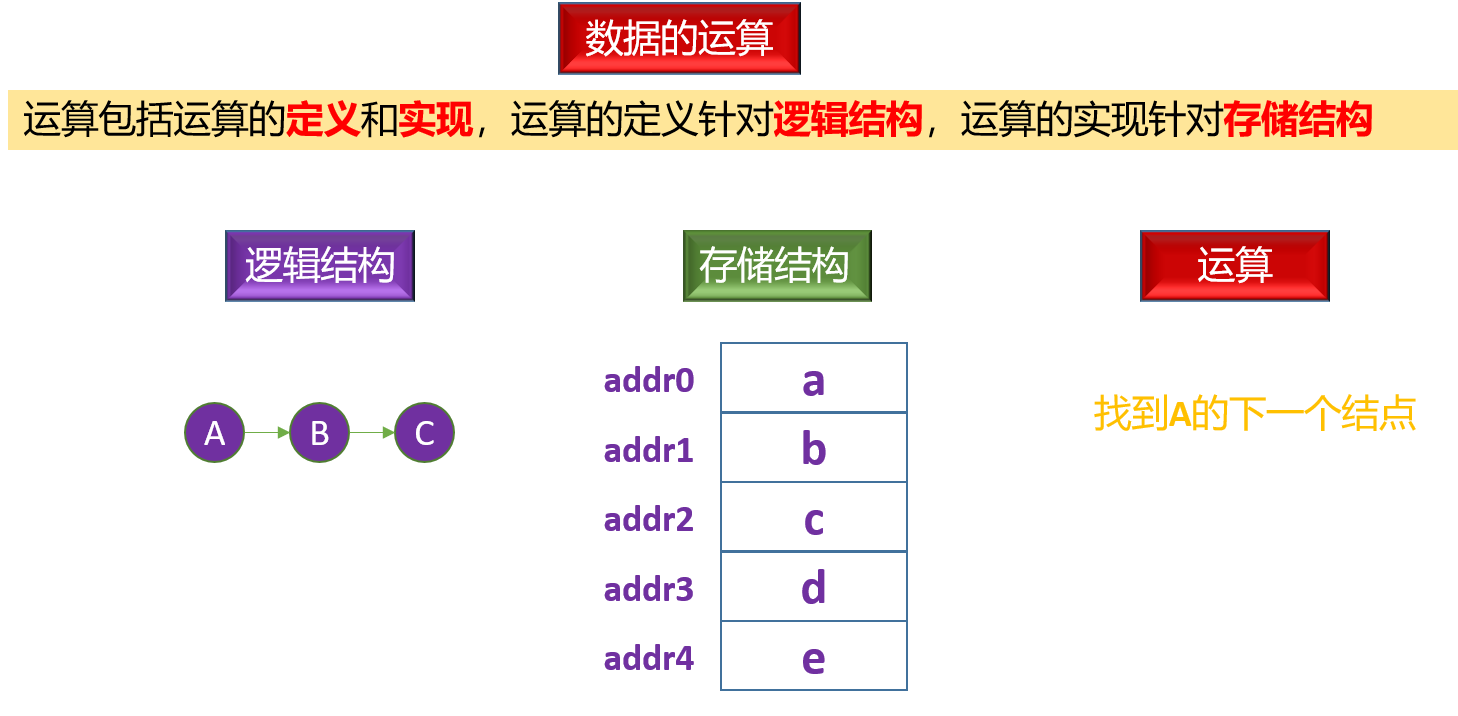
数据结构的定义(DS)+算法评价方法+ADT 描述形式
| [单选] 数据在计算机存储器内表示时,物理地址与逻辑地址相同并且是连续的,称之为()。 |
| A.存储结构 |
| B.逻辑结构 |
| C.顺序存储结构 |
| D.链式存储结构 |
| C |
| 【◆参考答案◆】:C |
1.基本术语
(1)数据:描述客观事物的数字、字符以及所有能输入到计算机中并被计算机程序处理的符号的集合。(数字、字符、声音、图形、图像等等)
(2)数据元素:数据的基本单位,在计算机程序中常常作为一个整体进行考虑和处理,如纪录/结构。
(3)数据项:数据的不可分割的最小单位,如结构中的域。
(4)数据对象:性质相同的数据元素的集合,是数据的一个子集。
2.数据结构
(1)定义:是相互之间存在一种或多种特定关系的数据元素的集合。
另一种定义:按照逻辑关系组织起来的一批据,按一定的存储方法把它存储在计算机中,并在这些据上定义了一个运算的集合。
(2)四种基本结构(逻辑结构)
集合:元素仅属于同一个集体,没有其他关系。
能线性结构:存在一对一关系,序列相邻,次序关系。
树型结构:存在一对多关系,层次关系
图状结构(网状结构):存在多对多关系,任意性。
存储器模型:一个存储器M是一系列固定大小的储单元
每个单元U有一唯一的地址A(U),该地址被连地编码
每个单元U有一个唯一的后继单元U'=succ(U)
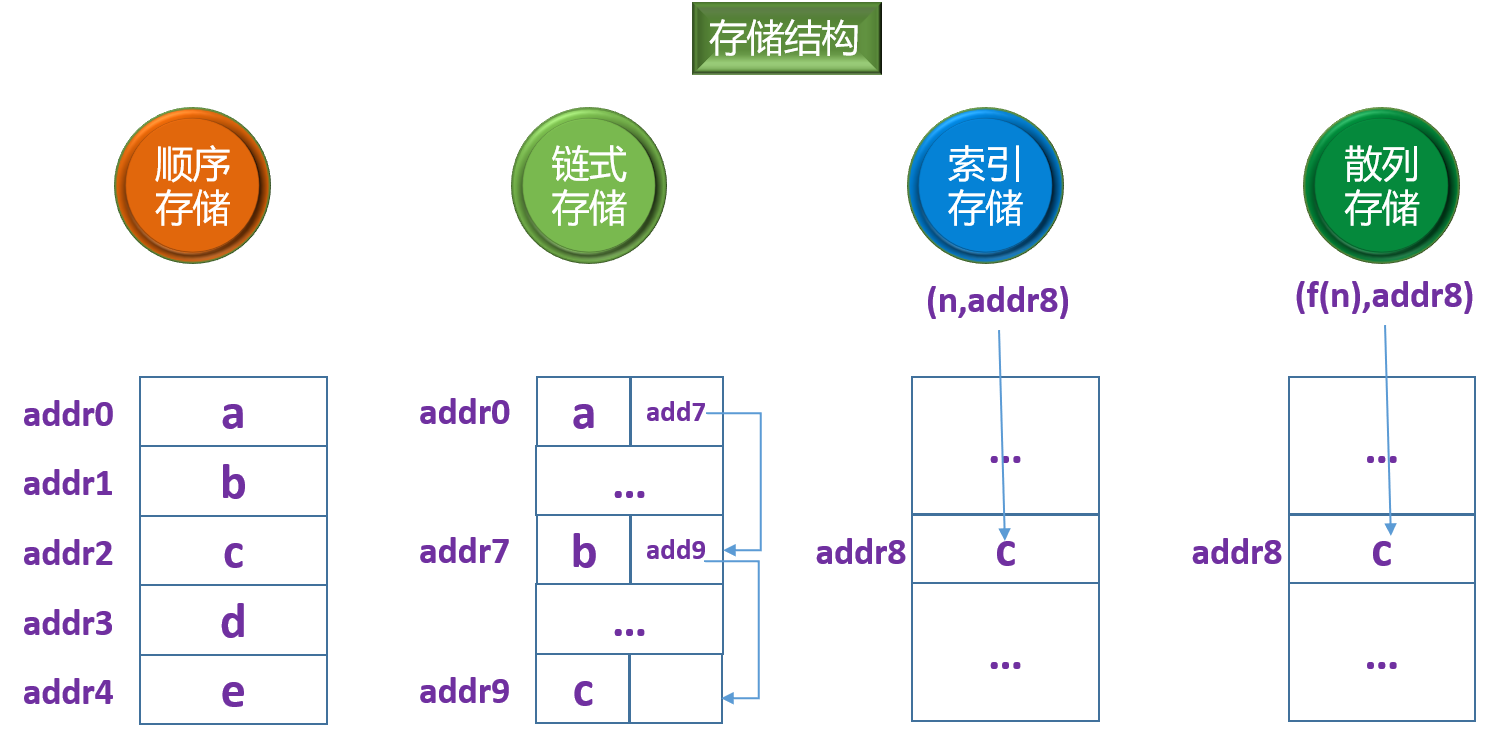
四种存储结构:顺序存储、链接存储、索引存储、散列存储
3.数据结构的划分
(1)按数据结构的性质划分
集合:元素仅属于同一个集体,没有其他关系。
数据的逻辑结构一数据元素之间的逻辑关系
(设计算法一数学模型)。数据的物理结构一数据结构在计算机中的映像
(存储结构,算法的实现)
1)____是组成数据的基本单位,是数据集合的个体。
数据元素
定义:是指基于一个逻辑类型的数据模型以及定义在该模型上的一组操作。每一个操作由它的输入和输出定义。
抽象的与具体的相对应
示例:
int a,b;则a和b可以进行+,一,*,/的运算
2和6则是具体的int数据
数据结构的三要素
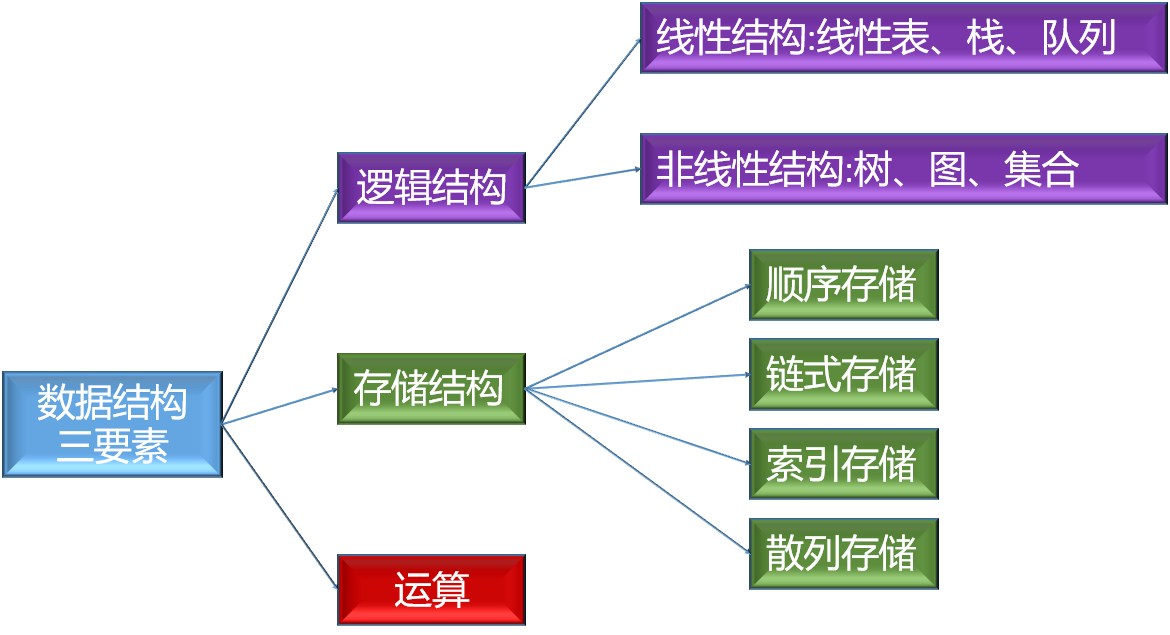

给出四种基本数据结构名称及其关系图示。
线性结构,集合结构,树形结构,图形结构
1.算法
定义:指一系列确定的而且是在有限步骤内能完成的操作。
3 .算法设计的要求
( 1) 正确性
( 2 )可读性
首先是给人读,然后才是机器执行
( 3 )健壮性容错性
( 4 )效率与低存储量需求
2.算法与数据结构的关系
数据计算机科学家沃斯(N.Wirth)提出的:
"算法+数据结构=程序”
揭示了程序设计的本质:实问题选择了种好的数据
结构,加上设计一个好的《于描述际问题的数据结构。算与数据结构是互相互相系的。
一个算法总是建立在一定数据结构上的:反之,算法不确
定,就无法决定如何构造数据。
如何设计一个“好”的算法
正确性 算法应能够正确地解决求解问题
可读性 算法应具有良好的可读性,以帮助人们理解
健壮性 输入非法数据时,算法能适应的做出反应或进行处理
效率与存储量 效率是指算法执行时间,存储量需求是指算法执行过程中所需最大存储空间
算法与数据结构关系举例
例1:编写程序查询某城市某人的电话号码建立一张登记表,
存放2个数据项:
姓名+Te1
好的算法取决于这张表的结构及存储方式:
√将出结点照姓名顺序地存储在计算机中,依次查找,
√建立一张姓氏引表:姓+表中的起始地址则不需查找其他
姓氏,查找效得到提高。
算法与数据结构关系举例
总结
解决问题的关键步骤是先选取合适的数据结构表示问题,才能写出有效的算法。
|
23.数据结构王道考研第一章:绪论.第二节:算法和算法评价第7页,第一.3题[2011年计算机联考真题] 设n是描述问题规模的非负整数,下面程序片段的时间复杂度是( ) 。
x=2 ; while (x<n/2) x=2*x ; |
| A. O(log2n) |
| B . O(n) |
| C. O(nlog2n) |
| D . O(n²) |
| A |
|
A. [解析] 1.找出基本操作一-最深层 循环内的语句。 2.找出问题规模并确定关于n的函数式。 初始(第0轮) x=2 第1轮循环结束x=4 第2轮循环结束x=8 第3轮循环结束x=16 发现x=2, 4, 8, 16, 32...... 第k轮循环结束x=2k+l, 不再进入第k+1轮。 循环体执行第k次之后,x=2k+1, while条件要求x<n/2,此时若不满足while条件,则x=2k+1>=n/2, k>=logzn-2,时间复杂度0(log2n) |
|
23.数据结构王道考研第一章:绪论.第二节:算法和算法评价第7页,第一.5题[2013年计算机联考真题] 已知两个长度分别为m和n的升序链表,若将它们合并为一个长度为m+n的降序链表,则最坏情况下的时间复杂度是()。
|
| A. O(n) |
| B . O(mxn) |
| C . O(min(m, n)) |
| D . O(max(m, n)) |
| D |
|
D.1.将链表从升序合并后变为降序,采用头插法比较方便。 2.每次取出m和n中剩下的最小元素,插入到head结点后,类似于归并排序的思想。若某一个表比较完毕,另一个表的余下元素直接依次用头插法插入到头结点后。
最坏情况: 两个表中元素依次比较,时间复杂度为O(max(m,n)) 推广:O(max(m, n))=O(m+n) |
|
23.数据结构王道考研第一章:绪论.第二节:算法和算法评价第7页,第一.5题[2014年计算机联考真题]
下列程序段的时间复杂度是( ) 。
count=0; for(k=1;k <=n;k*=2) for(j=1;j<=n;j++) count+ +; |
| A. O(log2n) |
| B . O(n) |
| C . O(nlog2n) |
| D . O(n2) |
| C |
|
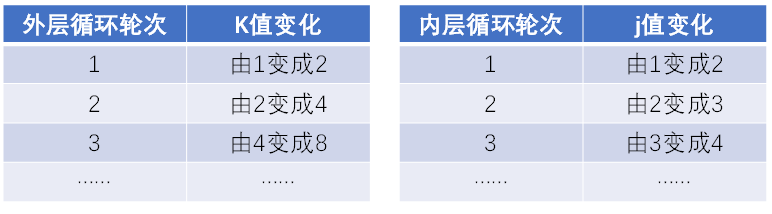
C基本操作: count++; 1.内外层循环相互独立(循环变量k和j互不影响),外层循环每执行一轮,内层都会完成一次完整的循环。
1.外层k=1,2,4,8,16…假设外层循环执行i次结束,不再进入第i+1次循环,k=2i>=n得到i>=log2n,则外层时间复杂度为0(log2n) 2.内层j=1,2,3,4, ....假设内层循环执行m次结束,不再进入第m+1次循环,则j=m+1>=n, 得到m>=n-1,则内层:时间复杂度为o(n) 3.由外相乘得到总时间复杂度为o(nlog2n) |
|
23.数据结构王道考研第一章:绪论.第二节:算法和算法评价第8页,第一.10题
以下算法中加下划线语句的执行次数为() Int m=0,I,j; for(i=1; i<=n; i++) for(j=1;j<=2*i;j++) m++; |
||||||||||||||||||
| A. n(n+1) | ||||||||||||||||||
| B.n | ||||||||||||||||||
| C. n+1 | ||||||||||||||||||
| D.n² | ||||||||||||||||||
| A | ||||||||||||||||||
A.2+4+6+…+2n=1/2(2+2n)×n=n(n+1) |
(三)算法效率的衡量方法和准则
一个特定算法的“运行工作量”的大小,只依赖于问题的规模(通常用整数量n表示)或者说,它是问题规模的函数。
假如,随着问题规模n的增长,算法执行时间的增长率和f(n)的增长率相同,则可记作:
T (n) = O(f(n))
称T (n)为算法的(渐近)时间复杂度。
如何估算算法的时间复杂度?
算法=控制结构+原操作
(固有数据类型的操作)
算法的执行时间=原操作(i)的执行次数X原操作(i)的执行时间
算法的执行时间与原操作执行次数之和成正比
对 数 函 数 く 幂 函 数 く 指 数 函 数
6.空间复杂度
(1)存储算法本身所占用的空间
(2)算法的输入/输出数据占用的空间
(3)算法在运行过程中临时占用的辅助空间
原地工作:若辅助空间相对于输入数据量是常数,则称算法是原地工作。
若所占空间量依赖于特定的输入,按最坏情况来分析
结构体:不同类型变量组合在一起构成的变量。
|
|
int*P=NULL;
void getResult (int *&P)
{
…
p=q;
…
}
调用: getResult (p) ;
p前加&定义成引用型,在*与变量名间加&
q的值就会变成p的值.
希望对变量改变,改变结果对我们来说很重要才定义成引用型(这种用c++方法)
C++转变成c语言
int result =0;
void getResult(int &r)
{
++r;
}
调用getResult(result);
↓ plainc
int result = 0;
void getResult(int *r)
{
++r;
}
调用getResult(&result);
int *p = NULL;
void getResult(int *p)
{
…
p = q;
…
}
调用getResult(p);
↓ plainc
int *p = NULL;
void getResult(int **p)
{
…
*p = q;
…
}
调用getResult(&p);
定义成指针的指针在变量名字前加两个**,(二级指针)
如下程序段:
for(i=1;i<=9;i++)
for(j=i+1;j<=10;j++)
i++;
其中语句x++执行的次数为
执行的语句频度为n(n-1)/2=10(10-1)/2=45次
4、当输入为abc#时,写出调用pr函数的输出结果。
#include<stdio.h>
#pragma warning(disable:4996)
void pr()
{
char ch;
scanf("%c", &ch);
if (ch != '#')pr();
printf("% c", ch);
}
int main()
{
pr();
return 0;
}
#cba
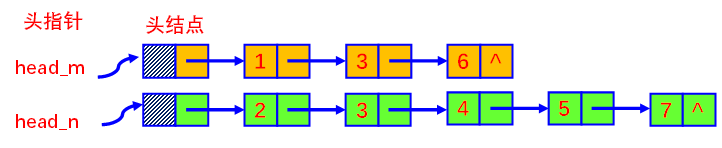
2、数据结构研究内容主要包括数据的逻辑结构和数据的物理结构。请分别简述逻辑结构和物理结构的含义,并简要指出线性表的两种常见物理结构。
逻辑结构
简单来说,数据的逻辑结构就是数据间的逻辑关系,而与他们在计算机中的存储位置无关。而按照数据间的关系,我们可以将逻辑结构分为线性结构和非线性结构。
物理结构
逻辑结构存储对象之间的关系,而物理结构指数据的逻辑结构在计算机存储空间的存放形式。通俗的讲,物理结构指的是数据在物理存储空间上选择集中存放还是分散存放,这很好理解。常见的存储结构有顺序存储、链式存储、索引存储以及散列存储(哈希表)。

评论列表 (0 条评论)