张宇八套卷错题
💮2021张宇8套卷第一套:第三.16题
16.二次型\(f(x_1,x_2,x_3)=2x_1x_2+2x_1x_3-6x_2x_3\)的正惯性指数为____.
所给的二次型不含平方项,故令\(x_1=y_1+y_2,x_2=y_1-y_2,x_3=y_3,\)有
\(f(x_1,x_2,x_3)=2y_1^2-2y_2^2-4y_1y_3+8y_2y_3,\)
再用配方法有
\(f(x_1,x_2,x_3)=2(y_1-y_3)^2-2(y_2-2y_3)^2+6y_3^2\)
令\(z_1=y_1-y_2,z_2=y_2-2y_3,z_3=y_3\),得
\(f(x_1,x_2,x_3)=2z_1^2-2z_2^2+6z_3^2\),又上述所作变化均为可逆线性变换,故其正惯性指数为2.
💮2021张宇8套卷第一套:第三.16题
19.在高为1m得圆柱形容器内存储某种液体,并将容器横放,圆得方程为\(x^2+y^2=1\)(单位:m)
(1)如果容器内存满了液体后,以\(0.2m^3/min\)的速率将液体从容器顶端抽出,当液面在y=0时,求液面下降的速率
(2)如果液体的密度为\(1N/m^3\)(单位体积液体的重力),求抽完全部液体需要作多少功?

(1)如图所示,当液面在\(y(-1\le y\le1)\)处时,容器内液体的体积为V=V(t),则
\(\frac{dV}{dt}=\frac{dV}{dt}\cdot\frac{dy}{dt}=2\sqrt{1-y^2}\frac{dy}{dt},\)
令y=0并由条件\(\frac{dV}{dt}=0.2得\frac{dy}{dt}=0.1(m/min),\)故液面下降得速率为0.1m/min.
(2)\(w=\int_{-1}^{1}2\sqrt{1-y^2}(1-y)dy\)
\(=\int_{-1}^{1}2\sqrt{1-y^2}dy-\int_{-1}^{1}2y\sqrt{1-y^2}dy\)
\(=4\int_{0}^{1}\sqrt{1-y^2} \)\(\color{red}{\overrightarrow{\quad y=sint\quad}}\)\(4\int_{0}^{\frac{\pi}{2}}cos^2tdt\)
\(=4\cdot\frac{\pi}{4}=\pi(J)\)
其中,由于\(2y\sqrt{1-y^2}dy\)为奇函数故\(\int_{-1}^{1}2y\sqrt{1-y^2}dy=0\)
\(\text{22.已知实矩阵}A= \begin{pmatrix}2&2\\2&a\\ \end{pmatrix} B= \begin{pmatrix}4&b\\3&1\\ \end{pmatrix} \text{a为正整数,若存在可逆矩阵C,使得}C^TAC=B. \\\)
\(\text{(1)求a,b的值;}\\\text{(2)求矩阵C}\\\)
注意:本题不是相似:而是合同
\((1)\text{因}A^T=A,\text{故}B^T=(C^TAC)^T=C^TA^TC=C^TAC=B,\text{所以B为对称矩阵,b=3,}\\\)
对于
\( f(x_1,x_2)=(x_1,x_2)\begin{pmatrix}2&2\\2&a\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}=2x_{1}^{2}+ax_{2}^{2}+4x_1x_2\\ =2(x_1+x_2)^2+(a-2)x_{2}^{2}\\\)
对于
\(g(y_1,y_2)=(y_1,y_2)\begin{pmatrix}4&3\\3&1\end{pmatrix}\begin{pmatrix}y_1\\y_2\end{pmatrix}=4y_{1}^{2}+y_{2}^{2}+6y_1y_2\\ =4\left(y_1+\frac{3}{4}y_2\right)^2-\frac{5}{4}y_{2}^{2}.\\\)
\( \text{由于A与B合同,故矩阵A与B得正、负指数对应相等,于是a-2<0,即a<2,又a为正整数,故a=1}\\ \text{综上所述:a=1,b=3}\\\)
\((2)\text{由(1)知,}\\ \text{令}\begin{cases}z_1=x_1+x_2\\z_2=x_2\end{cases}\text{,经过可逆线性变换}\begin{pmatrix}z_1\\z_2\\\end{pmatrix}=\begin{pmatrix}1&1\\0&1\\\end{pmatrix}\begin{pmatrix}x_1\\x_2\\\end{pmatrix}=C_1\begin{pmatrix}x_1\\x_2\\\end{pmatrix}\\ \)
\(\text{使}f(x_1,x_2)=2z_{1}^{2}-z_{2}^{2}\\ g(y_1,y_2)=4\left(y_1+\frac{3}{4}\right)^2-\frac{5}{4}y_{2}^{2}, \text{令}\begin{cases}z_1=\sqrt{2}y_1+\frac{3\sqrt{2}}{4}y_2\\z_2=\frac{\sqrt{5}}{2}y_2\\\end{cases}\\ \)
\(\text{即经可逆线性变换}\begin{pmatrix}z_1\\z_2\\\end{pmatrix}=\begin{pmatrix}\sqrt{2}&\frac{3\sqrt{2}}{4}\\0&\frac{\sqrt{5}}{2}\\\end{pmatrix}\begin{pmatrix}y_1\\y_2\\\end{pmatrix}=C_2\begin{pmatrix}y_1\\y_2\\\end{pmatrix}\\ \)
\(\text{使}\\ g(y_1,y_1)=2z_{1}^{2}-z_{2}^{2},\\ \)
\(\text{于是有}C_1\begin{pmatrix}x_1\\x_2\\\end{pmatrix}=C_2\begin{pmatrix}y_1\\y_2\\\end{pmatrix}\\ \)
\(\text{故}\begin{pmatrix}x_1\\x_2\\\end{pmatrix}=C_{1}^{-1}C_2\begin{pmatrix}y_1\\y_2\\\end{pmatrix}=C\begin{pmatrix}y_1\\y_2\\\end{pmatrix}\\\)
\( \text{即}C={\begin{pmatrix}1&1\\0&1\\\end{pmatrix}}^{-1}\begin{pmatrix}\sqrt{2}&\frac{3\sqrt{2}}{4}\\0&\frac{\sqrt{5}}{2}\\\end{pmatrix}\\ \)
\(=\begin{pmatrix}1&-1\\0&1\\\end{pmatrix}\begin{pmatrix}\sqrt{2}&\frac{3\sqrt{2}}{4}\\0&\frac{\sqrt{5}}{2}\\\end{pmatrix}\\ =\begin{pmatrix}\sqrt{2}&\frac{3\sqrt{2}-2\sqrt{5}}{4}\\0&\frac{\sqrt{5}}{2}\\\end{pmatrix}\\\)
|
💮2021张宇8套卷第二套:第一.8题 8.设函数f(x)在区间[0,+∞)上一阶导数连续,f(0)=1,且对任意t>0,曲线y=f(x)与直线x=0所围成的图形的面积与曲线y=f(x)在[0,t]上的一段弧长相等,则f(x)为() |
| \(A.\frac{e^x+e^{-x}}{2}\) |
| \(B.\frac{e^x-e^{-x}}{2}\) |
| \(C.e^x-e^{-x}\) |
| \(D.{e^x+e^{-x}}\) |
| A |
|
答案A.曲线y=f(x)与直线x=0,x=t,y=0所围成得图形面积为\(\int_{0}^{t}|f(x)|dx,曲线y=f(x)\),在[0,t]上得一段弧长度为\(\int_{0}^{t}\sqrt{1+[f'(x)]^2}dx.\) 根据条件,知 \(\int_{0}^{t}|f(x)|dx=\int_{0}^{t}\sqrt{1+[f'(x)]^2}dx.\) 两边对t求导,得\(|f(t)|=\sqrt{1+[f'(t)]^2},\)即\(f^2(t)=1+[f'(t)]^2,\)即\(f^2(x)=1+[f'(x)]^2,\)则 \(y'=\pm\sqrt{y^2-1},\) 解得\(ln[C(y+\sqrt{y^2-1})]=\pm x,\)再由f(0)=1可解得C=1,因此\(y+\sqrt{y^2-1}=e^{\pm x},\)由此解得 \(f(x)=\frac{e^x+e^{-x}}{2}\) |
💮2021张宇8套卷第二套:第二.14题
14.设函数f(x)再(0,+∞)上连续,且对任意正值a与b,积分\(\int_{a}^{ab}f(x)dx\)的值与a无关,且f(1)=1,则f(x)=___
答案:\(\frac{1}{x}(x>0)\)
解析:由\(\int_{a}^{ab}f(x)dx\)与a无关所以\(\left[\int_{a}^{ab}f(x)dx\right]'\equiv0,\)即
\(f(ab)b-f(a)\equiv0.\)
上式对任意a均成立,所以令a=1亦成立,有\(f(b)b-f(1)=0,f(b)=\frac{1}{b},\)即有\(f(x)=\frac{1}{x}(x>0)\)
可以验算,\(\int_{a}^{ab}\frac{1}{x}dx=ln(ab)-lna=lnb,\)与a无关
💮2021张宇8套卷第二套:第三.16题
17.已知y=y(x)(x>0)由方程\(y^3=x(x^2-2y)\)所确定,且曲线y=y(x)有斜近线y=ax+b,求a,b的值
解:由\(a=\lim\limits_{x\to+\infty}\frac{y}{x},\)令\(\frac{y}{x}=u,\)则y=ux,代入\(y^3=x(x^2-2y)\),得\(u^3x^3=x(x^2-2ux),\)即
\(u^3=1-\frac{2u}{x},\)
两端取极限,有\(\lim \limits_{x\to+\infty}u^3=\lim \limits_{x\to+\infty}(1-\frac{2u}{x}),\)即\(\lim\limits_{x\to+\infty}(\frac{y}{x})^3=\lim\limits_{x\to+\infty}(1-2\cdot\frac{y}{x}\cdot\frac{1}{x}),\)得
\(a^3=1-2\cdot a\cdot 0, \)即a=1.
又\(b=\lim\limits_{x\to+\infty}(y-ax)=\lim\limits_{x\to+\infty}(y-x)\),令y-x=t,代入\(y^3=x(x^2-2y)\),得
\((x+t)^3=x[x^2-2(x+t)]\)
整理得:\(y^3+3x^2t+3xt^2=-2xt-2x^2\)
两端除以\(x^2\)有,\(\frac{t^3}{x^2}+3t+\frac{3t^2}{x}=-2\frac{t}{x}-2\)
两端再取极限,有\(\lim\limits_{x\to\infty}\left(\frac{t^3}{x^2}+3t+\frac{3t^2}{x}\right)=\lim\limits_{x\to\infty}\left(-2\frac{t}{x}-2\right)\)
即\(\lim\limits_{x\to\infty}\left[\frac{(y-x)^3}{x^2}+3(y-x)+\frac{3(y-x)^2}{x}\right]=\lim\limits_{x\to\infty}\left(-2\frac{y-x}{x}-2\right)\)
得3b=-2,即\(b=-\frac{2}{3}\).
💮2021张宇8套卷第二套:第三.21题
22.(1)证明当x<0时,\(e^x(x^2+2)<2\);
(2)记函数\(f(x)=max\{e^{-x}, \frac{1}{2}x^2+1\},\)若可导函数g(x)≥f(x).x∈R,证明g(0)>1.
(1)令\(h(x)=e^x(x^2+2)-2,\)则h(0)=0,且
\(h'(x)=e^x(x^2+2x+2)=e^x[(x+1)^2+1]>0\)
故h(x)再(-∞,+∞)上单调增加,当x<0时,h(x)<h(0)=0,即\(e^x(x^2+2)<2\).
(2)由(1)知,当x≥0时,\(e^x(x^2+2)\ge2.\)因此当x<0时,\(\frac{1}{2}x^2+1<e^{-x}\);当x≥0时,\(\frac{1}{2}x^2+1\ge e^x\),
故
\(f(x)=\begin{cases}e^{-x}, &x<0,\\\frac{1}{2}x^2+1,&x\ge 0, \end{cases}\)且\(g(0)\ge f(0)=1\)
若g(0)=1,则
\(g_{+}^{'}(0)=\lim\limits_{x\to0^+}\frac{g(x)-g(0)}{x-0}\ge \lim\limits_{x\to0^+}\frac{f(x)-f(0)}{x-0} = \lim\limits_{x\to0^+}\frac{\frac{1}{2}x^2+1-1}{x}=0\)
\(g_{-}^{'}(0)=\lim\limits_{x\to0^-}\frac{g(x)-g(0)}{x-0}\ge \lim\limits_{x\to0^-}\frac{f(x)-f(0)}{x-0} = \lim\limits_{x\to0^-}\frac{e^{-x}-1}{x}=-1\)
于是\(g_{+}^{'}(0)\not= g_{-}^{'}(0)\),g(x)在x=0处不可导,与题设矛盾,故g(0)>1.
💮2021张宇8套卷第二套:第三.22题
\(22.(1)\text{设二次型}f(x,y,z)=y^2+2xz,\text{用正交变换x=QY将其华为标准型,并写出Q}\\\)
\( (2)\text{求函数}g(x,y,z)=\frac{y^2+2xz}{x^2+y^2+z^2}(x^2+y^2+z^2\not=0)\text{最大值,并求出一个最大值点} \)
\(\text{解答} (1)f(x,y,z)=x^T \begin{pmatrix}0&0&1\\0&1&0\\1&0&0\\ \end{pmatrix}x,\text{其二次型矩阵}A=\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\\\end{pmatrix} x=(x,y,z)^T,\)
\(\text{令}\\ |\lambda E-A|=\begin{vmatrix}\lambda&0&-1\\0&\lambda-1&0\\-1&0&1\\\end{vmatrix}=(\lambda-1)^2(\lambda+1)=0 \text{得A的特征值}\lambda_1=\lambda_2=1,\lambda_3=-1.\\ \)
\(\text{当}\lambda_1=\lambda_2=1,\\ (E-A)x=\begin{pmatrix}1&0&-1\\0&0&0\\-1&0&1\\\end{pmatrix}x=0\\\)
\( \text{得线性无关得特征向量}\xi_1=(1,0,1)^T,\xi_2=(0,1,0)^T,\\\)
\( \text{当}\lambda_3=-1, (-E-A)x=\begin{pmatrix}-1&0&-1\\0&-2&0\\-1&0&-1\\\end{pmatrix}x=0\\ \text{得线性无关得特征向量}\)
\(\xi_3=(1,0,-1)^T\\ \xi_1,\xi_2,\xi_3\text{已经正交,只需要单位化}\\ \eta_1=(\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}})^T, \eta_2=(0,1,0)^T, \eta_3=(\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}})^T, \\\)
\(\text{令} Q=(\eta_1,\eta_2,\eta_3)=\begin{pmatrix}\frac{1}{\sqrt{2}}&0&\frac{1}{\sqrt{2}}\\0&1&0\\\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\end{pmatrix} \text{即为所求得正交矩阵}.\\\)
\( \text{记}y=(u,v,w)^T,\text{则经过正交变换}x=Qy,\)
\(\text{有} f(x,y,z)=x^TAx=y^TQ^TAQy=y^T\begin{pmatrix}1&&\\&1&\\&&-1\\\end{pmatrix}y=u^2+v^2-w^2.\\\)
\((2)\text{由}(1),f\le u^2+y^2+z^2,\text{又}\\ x^2+y^2+z^2=x^Tx=(Qy)^T(Qy)=y^TQ^TQy=y^Ty=u^2+v^2+w^2,\\ \text{故},g(x,y,z)=\frac{f(x,y,z)}{x^2+y^2+z^2}\le \frac{u^2+v^2+w^2}{u^2+v^2+w^2}=1,\\ \)
\(\text{即函数g(x,y,z)得最大值为1,且当(u,v,w)=(0,1,0)时,g(x,y,z)=1.此时}\\ \)
\(\begin{pmatrix}x\\y\\z\\\end{pmatrix}=Q\begin{pmatrix}0\\1\\0\\\end{pmatrix}=\begin{pmatrix}\frac{1}{\sqrt{2}}&0&\frac{1}{\sqrt{2}}\\0&1&0\\\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\end{pmatrix}\begin{pmatrix}0\\1\\0\\\end{pmatrix}=\begin{pmatrix}0\\1\\0\\\end{pmatrix},\\ \)
\(\text{故g(x,y,z)得一个最大值点时(0,1,0)}.\)
|
💮2021张宇8套卷第三套:第一.2题 2.设函数\(f(x)=x^4-\frac{4}{3}x^3+2x^2+ax+b\)在(-∞,+∞)上有定义,其中a,b时常数,则 |
| A.对任意实数b,f(x)在区间(-∞,0)上单调减少 |
| B.对任意实数a,f(x)在区间(-1,+∞)上单调增加 |
| C.对无穷多个实数a,f(x)在区间(0,1)上单调减少 |
| D.对某个实数b,f(x)在(-∞,+∞)上单调函数. |
| C |
|
答案C.解析: 因为f(x)的常数项b不影响f(x)的单调性,所以可排除A,D又由于 \(f'(x)=4x(x^2-x+1)+a=4x\left[(x-\frac{1}{2})^2+\frac{3}{4}\right]+a,\) 且当x∈(0,1)时,有 \(0<4x\left[(x-\frac{1}{2})^2+\frac{3}{4}\right]<4\) 所以,当x∈(0,1)时,a<-4,f'(x)在(0,1)上单调减少,故选C. |
|
💮2021张宇8套卷第三套:第一.3题 3.设函数\(f(x)=\max\limits_{0\le y\le1}\frac{|x-y|}{x+y+1}, 0\le x\le1,\)则f(x)在[0,1]上的最小值与最大值分别为 |
| A.\(0,2-\sqrt{3}\) |
| B.\(0,\frac{1}{2}.\) |
| C.\(\frac{\sqrt{3}-1}{2}, \frac{1}{2}\) |
| D.\(2-\sqrt{3},\frac{1}{2}\) |
| D |
|
答案D. 分析:任意固定x∈(0,1),分别考虑\(\frac{|x-y|}{x+y+1}\)在区间[0,x],(x,1]上最大值. 当0≤y≤x时,\(\frac{|x-y|}{x+y+1}=\frac{x-y}{x+y+1}=\frac{2x+1}{x+y+1}-1\),关于y单调减少,所以 \(\max\limits_{0\le y\le1}\frac{|x-y|}{x+y+1}=\frac{x-y}{x+y+1}|_{y=0}=\frac{x}{x+1};\) 当x<y≤1时,\(\frac{|x-y|}{x+y+1}=\frac{y-x}{x+y+1}=1-\frac{2x+1}{x+y+1}\),关于y单调增加,所以 \(\max\limits_{0\le y\le1}\frac{|x-y|}{x+y+1}=\frac{y-x}{x+y+1}|_{y=1}=\frac{1-x}{x+2}.\) 注意到 \(\frac{x}{x+1}\le \frac{1-x}{x+2} \Leftrightarrow 0<x\le \frac{\sqrt{3}-1}{2}\) 又\(f(0)=f(1)=\frac{1}{2}\),因此f(x)可用分段函数表示为: \(f(x)= \begin{cases}\frac{1-x}{x+2},&0\le x \le \frac{\sqrt{3}-1}{2},\\\frac{x}{x+1},&\frac{\sqrt{3}-1}{2}<x\le 1.\end{cases}\) 当\(0\le x \le \frac{\sqrt{3}-1}{2}\)时,\(f(x)=\frac{1-x}{x+2}\)单调减少, 当\(\frac{\sqrt{3}-1}{2}<x\le 1\)时,\(f(x)=\frac{x}{x+1}\)单调增加. 又f(x)在[0,1]上连续,\(f(0)=f(1)=\frac{1}{2}\),\(f(\frac{\sqrt{3}-1}{2})=2-\sqrt{3}\),因此f(x)在[0,1]上的最小值为\(2-\sqrt{3}\),最大值为\(\frac{1}{2}\) 故选D |
💮2021张宇8套卷第三套:第三.18题
18.设函数f(x)在区间[a,b]上具有连续导数,f'(x)>0,且a≤f(x)≤b.求证:
(1)对任意\(x_1,x_2\in(a,b)\)存在\(c\in(a,b)\),使得\(f'(c)=\sqrt{f'(x_1)f'(x_2)}\);
(2)存在\(\xi\in(a,b)\),使得\(f[f(a)]-f[f(b)]=[f'(\xi)]^2(a-b)\).
(1)若\(f'(x_1)=f'(x_2),\)则取\(c=x_1\)或\(x_2\),即得\(f'(c)=\sqrt{f'(x_1)f'(x_2)}\)
若\(f'(x_1)\not=f'(x_2)\),不妨设\(f'(x_1)<f'(x_2)\),则\(f'(x_1)<\sqrt{f'(x_1)f'(x_2)}<f'(x_2).\)根据连续函数介质定理存在\(c\in(a,b)\),使得\(f'(c)=\sqrt{f'(x_1)f'(x_2)}\)
(2)因为f'(x)>0,所以\(a\le f(a)<f(b)\le b.\)对f(x)在区间[a,b]与[f(a),f(b)]上用拉格朗日中值定理,存在\(\eta_1 \in(a,b),\eta_2\in(f(a), f(b))\),使得
\(f(b)-f(a)=f'(\eta_1)(b-a),\)
\(f[f(a)]-f[f(b)]=f'(\eta_2)[f(b)-f(a)]\)
由此得
\(f[f(a)]-f[f(b)]=f'(\eta_1)f'(\eta_2)(a-b)\)
由(1)知,存在\(\xi\in(a,b)\)使得\(f'(\xi)=\sqrt{f'(\eta_1)f'(\eta_2)}\),代入公式,即得
\(f[f(a)]-f[f(b)]=[f'(\xi)]^2(a-b)\)
💮2021张宇8套卷第四套:第二.16题
18.若可逆矩阵D满足\(D^TD=\begin{pmatrix}1&-1&1\\-1&2&-3\\1&-3&6\\\end{pmatrix},\)则D=______.
分析:记\(\begin{pmatrix}1&-1&1\\-1&2&-3\\1&-3&6\\\end{pmatrix}=A\),则所对应的二次型为
\(f(x_1,x_2,x_3)=x^TAx=x_{1}^{2}+2x_{x}^{2}+6x{3}^{2}-2x_1x_2+2x_1x_3-6x_2x_3\)
\(=(x_1-x_2+x_3)^2+(x_2-2x_3)^2+x_{3}^{2}\)
\(=(x_1-x_2+x_3,x_2-2x_3,x_3)\begin{pmatrix}x_1-x_2+x_3\\ x_2-2x_3\\ x_3 \end{pmatrix}\)
\(=(x_1,x_2,x_3)\)\(\begin{pmatrix}1&0&0\\-1&1&0\\1&-2&1\\\end{pmatrix}\)\(\begin{pmatrix}1&-1&1\\0&1&-2\\0&0&1\\\end{pmatrix}\)
\(=(x_1,x_2,x_3)D^TD\begin{pmatrix}x_1\\x_2\\x_3\\\end{pmatrix}\)
其中\(A=D^TD,D=\begin{pmatrix}1&-1&1\\0&1&-2\\0&0&1\\\end{pmatrix}\)
💮2021张宇8套卷第四套:第二.22题
22.设a,b,c,d为常数,其中b≠0,矩阵\(A=\begin{pmatrix}a&b\\ c&d\\\end{pmatrix}\)的二重特征值为\(\lambda\),求可逆矩阵P,使得\(P^{-1}AP=\begin{pmatrix}\lambda&1\\0&\lambda\end{pmatrix}.\)
记\(P=\begin{pmatrix}x_1&x_2\\x_3&x_4\end{pmatrix},\)由题知\(a+d=\lambda+\lambda,\)即\(a-\lambda=\lambda-d,\)
由\(AP=P\begin{pmatrix}\lambda&1\\0&\lambda\end{pmatrix}\),有
\(\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}x_1&x_2\\x_3&x_4\end{pmatrix}\)\(=\begin{pmatrix}x_1&x_2\\x_3&x_4\end{pmatrix}\begin{pmatrix}\lambda&1\\0&\lambda\end{pmatrix}\),
即\(\begin{cases}ax_1+bx_3=\lambda x_1,\\ ax_2+bx_4=x_1+\lambda x_2,\\ cx_1+dx_3=\lambda x_3,\\ cx_2+dx_4=x_2+\lambda x_4,\\ \end{cases}\)
化简得\(\begin{cases}(a-\lambda)x_1+bx_3= 0,\\ -x_1+(a-\lambda)x_2+bx_4=0,\\ cx_1+(d-\lambda)x_3= 0,\\ cx_2-x_3+(d-\lambda)x_4=0,\\ \end{cases} (*)\)
又因\(\lambda\)是A得二重特征值,故\(\begin{pmatrix}\lambda-a&-b\\-c&\lambda-d\end{pmatrix}=0\)
对于方程组(*)的系数做初等行变换,得
\(\begin{pmatrix}a-\lambda&0&b&0\\-1&a-\lambda&0&b\\c&0&d-\lambda&0\\0&c&-1&d-\lambda\end{pmatrix}\)
\(\begin{matrix} r3+\frac{\lambda-d}{b}\\ \overrightarrow{\quad r_3\leftrightarrow r_4 \quad}\\ \end{matrix} \begin{pmatrix}a-\lambda&0&b&0\\-1&a-\lambda&0&b\\0&c&-1&d-\lambda\\0&0&0&0\end{pmatrix}\)
\( \overrightarrow{\quad r_3+\frac{\lambda-d}{b}r_2 \quad} \begin{pmatrix} a-\lambda&0&b&0\\ -1&a-\lambda&0&b\\ \frac{d-\lambda}{b}&0&-1&0\\ 0&0&0&0 \end{pmatrix}\)
\( \overrightarrow{\quad r_3+\frac{1}{b}r_1 \quad} \begin{pmatrix} a-\lambda&0&b&0\\ -1&a-\lambda&0&b\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix}\)
则基础解系为\(\xi_1=\)\(\begin{pmatrix}b\\ 0\\ \lambda-a\\ 1 \end{pmatrix}\),\(\xi_2=\begin{pmatrix} 0\\ b\\ 0\\ a-\lambda\\ \end{pmatrix}\)
故通解为:
\(\begin{pmatrix}x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix}=k_1\xi_1+k_2\xi_2=\begin{pmatrix} k_1b\\ k_2b\\ k_1(\lambda-a)\\ k_1+k_2(\lambda-q) \end{pmatrix},\)
又\(\lambda-a=\frac{1}{2}(d-a),\)故所求矩阵为
\(p=\begin{pmatrix}k_1b&k_2b\\ \frac{1}{2}k_1(d-a)&k_1+k_2(d-a) \end{pmatrix},\)|\(|p|=k_{1}^{2}b\not=0,\)
其中\(k_1\not=0,k_2\)为任意常数
|
💮2021张宇8套卷第五套:第一8题 8.由曲线\(y=\sqrt{2x-x^2}\)与直线y=x围成得屏幕图形绕直线x=2旋转一周得到得旋转体体积为 |
| A.\(\frac{\pi^2}{2}+\frac{2\pi}{3}\) |
| B.\(\frac{\pi^2}{2}+\frac{4\pi}{3}\) |
| C.\(\frac{\pi^2}{2}-\frac{2\pi}{3}\) |
| D.\(\frac{\pi^2}{2}-\frac{4\pi}{3}\) |
| C |
|
8.C.解析: 以原横轴负方向新的纵轴方向、原来的直线x=2为新的横轴建立新的直角坐标(如图),所给平面图形在新的坐标系中可表示为 \(2-x\le y\le 1+\sqrt{1-x^2} (0\le x\le 1).\) 因此旋转体体积为 \(V=\pi \int_{0}^{1}(1+\sqrt{1-x^2})^2dx-\pi\int_{0}^{1}(2-x)^2dx\) \(=2\pi\int_{0}^{1}\sqrt{1-x^2}dx-2\pi\int_{0}^{1}(x-1)^2dx\) \(=2\pi\cdot\frac{\pi}{4}-2\pi\cdot\frac{1}{3}\) \(=\frac{\pi^2}{2}-\frac{2\pi}{3}.\) |
|
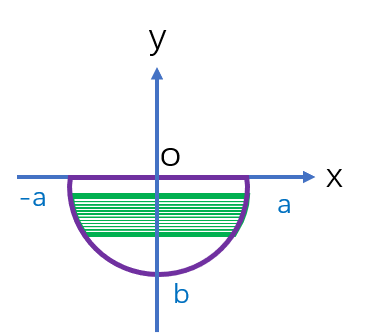
💮2021张宇8套卷第六套:第一.4题 4.有一椭圆行薄板,长、短分别为a与b,薄板垂直立于液体中,其长度与液体相齐,设液体的比重为\(\gamma\),则液体对薄板的侧面压力为() |
| A.\(\frac{2}{3}\gamma a^2b.\) |
| B.\(\frac{2}{3}\gamma ab^2.\) |
| C.\(\frac{4}{3}\gamma ab^2.\) |
| D.\(\frac{4}{3}\gamma a^2b.\) |
| B |
|
答案B.
分析:取水平条(如图),面积为dA=2xdy,此水平条上压力为 \(dP=2\gamma yxdy,\) 整个半椭圆的薄板所受侧压力为 \(p=\int_{0}^{b}2\gamma yxdy.\) 以椭圆方程\(x=\frac{a}{b}\sqrt{b^2-y^2}\)代入,得 \(P=\frac{2a\gamma}{b}\int_{0}^{b}y\sqrt{b^2-y^2}dy=\frac{2}{3}\gamma ab^2.\) 故选B. |
|
💮2021张宇8套卷第六套:第一.4题 9.设A是3阶实对称矩阵,满足\(A+A^2+\frac{1}{2}A^3=O\),则关于A的秩必有 |
| A.r(A)=0 |
| B.r(A)=1 |
| C.r(A)=2 |
| D.r(A)=3 |
| A |
|
答案A. 分析:设\(\lambda\)是A的任一特征值,,则\(\lambda+\lambda^2+\frac{1}{2}\lambda^3=0,\)解得\(\lambda=0\)或\(\lambda = -1\pm i,\)其中i是虚数单位.因为A是实对称矩阵,其特征值\(\lambda\)为实数,所以只能有\(\lambda_0=0\)(三重),并且A相似于对角矩阵\(\begin{pmatrix}\lambda_0&&\\&\lambda_0&\\&&\lambda_0\end{pmatrix}\),故r(A)=0,故选A. |
| 设\(f(x)=\int_{0}^{x}e^{-t}\frac{t(t+2)}{(t+3)^2}dt\) |
| A.有1个极小值,1个极大值,1条渐近线 |
| B.有1个极小值,1个极大值,2条渐近线 |
| C.有2个极小值,1个极大值,2条渐近线 |
| D.有2个极小值,2个极大值,2条渐近线 |
| B |
|
[分析]\(f'(x)=e^{-x}\frac{t(t+2)}{(t+3)^2}dt\overrightarrow{\quad 令 \quad}0\) \(x_1=2, x_2=0\) \(x_1=2\Rightarrow f'(x)\)由正变负\(\Rightarrow\)极大
\(x_2=0\Rightarrow f'(x)\)由负变正\(\Rightarrow\)极小 所以有1个极小值,1个极大值 \(\lim\limits_{x\to-3+0}f(x)=\lim\limits_{x\to-3+0}\int_{0}^{x}e^{-t}\frac{t(t+2)}{(t+3)^2}dt与\int_{0}^{-3}\frac{1}{(t+3)^2}dt\)同敛散 \(\lim\limits_{x\to-3+0}\frac{e^{-t}\frac{t(t+2)}{(t+3)^2}}{\frac{1}{(t+3)^2}}=e^3\cdot(-3)\cdot(-1)=A\not=0\) \(\int_{0}^{-3}\frac{1}{(t+3)^2}dt\overrightarrow{\quad t+3=u \quad} \int_{3}^{0}\frac{1}{u^2}du=-\int_{0}^{3}\frac{1}{u^2}du=\frac{1}{u}|_{0}^{3}=\frac{1}{3}-(+\infty)=-\infty\) 一个垂直渐近线 又\(\lim\limits_{x\to-3+0}f(x)=\lim\limits_{x\to-3+0}\int_{0}^{x}e^{-t}\frac{t(t+2)}{(t+3)^2}dt=\int_{0}^{+\infty}e^{-t}\frac{t(t+2)}{(t+3)^2}dt\) 由于 \(\lim\limits_{t\to+\infty}\frac{e^{-t}\frac{t(t+2)}{(t+3)^2}}{e^{-t}}=1\)与\(\int_{0}^{+\infty}e^{-t}dt\)同敛散 一个水平渐近线 |
|
💮2021张宇8套卷第七套:第一.10题 10.设A,B是n阶实对称,则存在n阶逆矩阵P,使得下列关系式 ①\(PA=B\)②\(p^{-1}ABP=BA\) ③\(P^{-1}AP=B;\)④\(P^{T}A^2P=B^2\) 成立的个数是() |
| A.1 |
| B.2 |
| C.3 |
| D.4 |
| C |
|
10. [答案] C 因为A,B均是n阶可逆矩阵,可取P=A.则有\(A^{-1}ABA=(A^{-1}A)BA=BA\),故②式成立。 |
💮2021张宇8套卷第七套:第二.17题
10.设\(f(x,y)=3x+4y-ax^2-2ay^2-2bxy.\)当a,b满足任何条件时,f(x,y)有唯一的极大值,并说明理由
17.解:由极值条件,得方程组
\(\begin{cases}\frac{\partial f}{\partial x}=3-2ax-2by=0\\ \frac{\partial f}{\partial y}=4-4ay-2bx=0\\ \end{cases}\)
整理得
\(\begin{cases}2ax+2by=3\\ bx+2ay=2\\ \end{cases}\)
当\(\begin{vmatrix}2a&2b\\ b&2a\\ \end{vmatrix}=4a^2-2b^2\not=0,\)即\(2a^2-b^2\not=0,\)方程由唯一解
\(x_0=\frac{3a-2b}{2a^2-b^2}, y_0=\frac{4a-3b}{4a^2-2b^2},\)
又由于\(A=\frac{\partial^2f}{\partial x^2}|_{(x_0,y_0)}=-2a\),\(B =\frac{\partial^2f}{\partial x \partial y}|_{(x_0,y_0)}=-2b\),\(C =\frac{\partial^2f}{\partial y^2}|_{(x_0,y_0)}=-4a\)
故当\(AC-B^2=8a^2-4b^2>0,\)且\(A=-2a<0,\)即\(2a^2-b^2>0\)时f(x,y)有唯一的极大值.
综上所述,当\(2a^2-b^2>0\)且a>0时,f(x,y)有唯一极大值
💮2021张宇8套卷第八套:第二.11题
11.\(\lim\limits_{x\to\infty}\int_{-1}^{2}(arctan\:nx)^3dx=\)_____.
\(\int_{-1}^{2}(arctan\:nx)^3dx=\int_{1}^{2}(arctan\:nx)^3dx\)
\(=\frac{1}{n}\int_{n}^{2n}(arctan\:nx)^3dx=\frac{1}{n}(2n-n)(arctan\:\xi_n)^3\)
=\((arctan\:\xi_n)^3\)
其中\(n\le\xi_n\le2n\),因为\(\lim\limits_{n\to\infty}arctan\:n=\frac{\pi}{2},\)所以有
\(\lim\limits_{x\to\infty}\int_{-1}^{2}(arctan\:nx)^3dx=\lim\limits_{x\to\infty}(arctan\:\xi_n)^3=(\frac{\pi}{2})^3=\frac{\pi^3}{8}\)
💮2021张宇8套卷第八套:第三.18题
18.以yOz面上屏幕线段\(y=f(z)(z\ge0)\)绕z轴选择一周所成的旋转曲面与xOy面围成一个无上盖容器(如图),现以\(3cm^3/s\)的速率把水注入容器中,水面面级以\(\pi \:cm^2/s\)的增大,已知容器底面面积为\(16\pi\: cm^2,\)求曲线y=f(z)的方程.
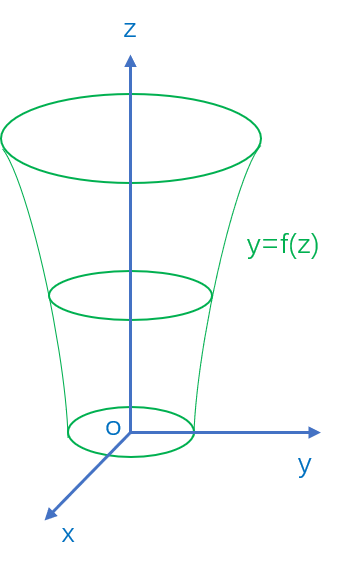
记t时刻容器哦水深为z(t),则注入水的体积为
\(V(t)=\int_{0}^{z(t)}\pi f^2(u)du,\)
水面的面积\(S(t)=\pi f^2(z),\)
由题意,
\(\frac{dV(t)}{dt}=\pi f^2[z(t)]\cdot \frac{dz}{dt}=3,\)
\(\frac{dS(t)}{dt}=\pi \cdot2f[z(t)]\cdot \frac{dz}{dt}=\pi,\)
故
\(\frac{df(z)}{dz}\cdot \frac{2}{f(z)}=\frac{\pi}{3},\)
分离变量得
\(\frac{df(z)}{f(z)}=\frac{\pi}{6}dz\)
于是\(\int\frac{df(z)}{f(z)}=\frac{\pi}{6}\int dz\)
得
\(ln|f(z)|=\frac{\pi}{6}z+lnc_1, \)\(f(z)=\pm c_1e^{\frac{\pi}{6}z}=ce^{\frac{\pi}{6}z}(z\le0),\)
又底面积为\(16\pi cm^2\),即f(0)=4,得c=4,即\(f(z)=4e^{\frac{\pi}{6}z}.\)
💮2021张宇8套卷第八套:第三.20题
20.设平面区域D是由封闭曲线\(x^2+y^2=a(x+\sqrt{x^2+y^2})\)所围成的有界闭区域,其中a>0,计算\(I=\iint_{D}[x^2ln(y+\sqrt{1+y^2})]+x\sqrt{x^2+y^2}d\sigma.\)
解:曲线\(x^2+y^2=a(x+\sqrt{x^2+y^2})\)是条什么曲线?采用极坐标.令
\(r=\sqrt{x^2+y^2},x=rcos\theta\),
于是该方程化为\(r=a(1+cos\theta),a>0,\)他是一条心形线,如图所示.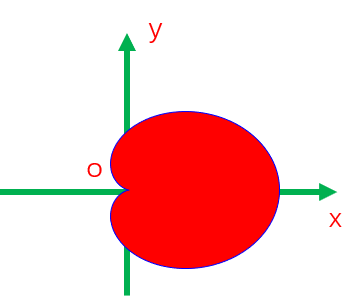
由于函数\(\varphi(x,y)=x^2ln(y+\sqrt{1+x^2})\)是关于y的奇函数,积分区域关于x轴对称,所以
\(\iint_{D}\varphi(x,y)d\sigma=0.\)
因此
\(I=\iint_D[x^2ln(y+\sqrt{1+y^2})+x\sqrt{x^2+y^2}]d\sigma\)
\(=\iint_Dx\sqrt{x^2+y^2}d\sigma\)
\(=\int_{0}^{2\pi}d\theta\int_{0}^{a(1+cos\theta)}r^3cos\theta dr\)
\(=\frac{\pi^4}{4}\int_{0}^{2\pi}(1+cos\theta)^4cos\theta d\theta\)
\(=\frac{\pi^4}{4}\int_{0}^{2\pi}(1+4cos\theta+6cos^2\theta+4cos^3\theta+cos^4\theta)cos\theta d\theta\)
\(=a^4\int_{0}^{\frac{\pi}{2}}(4cos^2\theta +4cos^4\theta)d\theta\)
\(=a^4(4×\frac{1}{2}×\frac{\pi}{2}+4×\frac{3}{4}×\frac{1}{2}×\frac{\pi}{2})=\frac{7}{4}\pi a^4\)
💮2021张宇8套卷第八套:第三.23题
22.设二次型\(f(x_1,x_2,x_3)=x^TA^*x\)可以用正交变换化为标准形\(f=2y_{1}^{2}-2y_{2}^{2}-y_{3}^{2},\)其中A*是3阶实对称矩阵A的伴随矩阵.
(1)求秩\(r(A^*+2E)\),其中E是3阶矩阵;
(2)已知二次型\(g(x_1,x_2,x_3)=x^TAx\)的正惯性指数为2,求行列式|A+2E|.
(1)根据题设条件,A*的特征值为\(\lambda=2,-2,-1,\)所以A+2E的特征值为4,0,1,故存在正交矩阵P,使得
\(P^{-1}(A^*+2E)P=\begin{pmatrix}4&0&0\\0&0&0\\0&0&1\\ \end{pmatrix}\)
因此r(A*+2E)=2.
(2)利用公式\(A^*A=|A|E\)两边取行列式,可得\(|A|^2=|A^*|=4\),所以\(A=\pm2.\)
若|A|=2,则\(A=|A|(A^*)^{-1}\)的特征值为\(\frac{|A|}{\lambda}:1,-1,-2;\)
若|A|=-2,则\(A=|A|(A^*)^{-1}\)的特征值为\(\frac{|A|}{\lambda}:-1,1,2.\)
因为二次型\(g(x_1,x_2,x_3)=x^TAx\)的真惯性指数为2,所以应该排除第一种情形,于是A+2E的特征值为1,3,4,行列式|A+2E|=1×3×4=12.
本文作者: 永生
本文链接: https://yys.zone/detail/?id=161
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明出处!
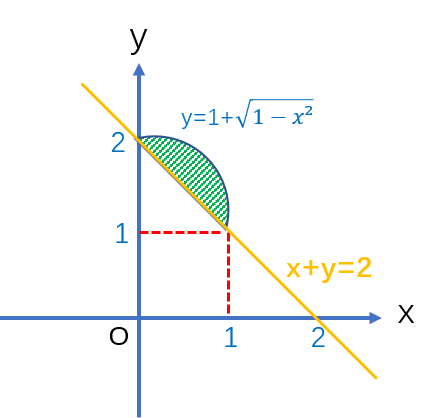
评论列表 (0 条评论)