第七章:查找(数据结构)
查找的目的是从给定的同一类型的数据集合中,找出
人们所需要的数据元素(或记录)。
基本术语:
记录(Record)、
关键字(Key word)、
主关键字(PrimaryKey)、
次关键字(Secondary Key) 、
查找表(SearchingTable)、
动态查找(Dynamic Searching)、
静态查找(Static Searching)、
内部排序(Internal Sorting)、
外部排序(External Sorting)、
稳定性(Stability)
查找(Searching):
所谓查找,是指在一个含有众多的数据元素(或记录)的查找表中,找出某个特定的数据元素(或记录)。
平均查找长度(Average Search Length)
给定待查找的关键字与查找表中关键字的比较次数
的期望值称为平均查找长度(简称:ASL)。
\(ASL=\sum_{n}^{i=1} P_i×c_i\)
其中:p i 为查找第i个元素的概率,且 =1。
ci 是指查找第i个元素所需进行的比较次数。
通常情况下,我们认为在查找表中,查找任意记录的概率是相等的。
查找表中数据元素的 形式定义为:
#define maxn 100 //maxn为表的最大长度
struct node
… {
elemtype key; //key为关键字,类型设定为elemtype
};
在对查找表实施静态查找时,查找表的组织结构可以是顺序表结构,也可以是单链表结构。下面我们介绍几种静态查找方法。
1、思想:
顺序查找是用待查找记录与查找表中的记录逐个比较,若找到相等记录,则查找成功,否则,查找失败。
2、 顺序查找算法实现
#define maxn 100 //maxn为表的最大长度
struct node
{…
elemtype key; //key为关键字,类型设定为elemtype;}
int seqsearch(snode &l,elemtype k)
{ int i=l.len;
l.R[0].key=k;
while(l.R[i].key!=k) //从表尾开始向前扫描
i--;
return i;}
在函数seqsearch中,若返回的值为0表示查找不成功,否则查找成功。函数中查找的范围从R[n]到R[1],R[0]为监视哨,起两个作用,其一,是为了省去判定 while循环中下标越界的条件i≥1,从而节省比较
时间,其二,保存要找值的副本,若查找时,遇到它,表示查找不成功。若算法中不设立监视哨R[0],程序花费的时间将会增加,这时的算法可写为下面形式。
int seqsearch(snode &l,elemtype k)
{
int i=l.len;
while((l.R[i].key!=k)&&(i>=1) )
i--;
return i;
}
3、性能分析:
假设对查找表的数据元素实施查找的概率相同即pi =1/n ,在查找表中查找第i个元素成功时的比较次数
Ci =i,查找第i个元素不成功时的比较次数Ci =n,则
对查找表实施顺序查找,在查找成功时的ASL为:
ASLSucc=?
假设在每个位置查找的概率相等,即有pi =1/n,由于查找是从后往前扫描,则有每个位置的查找比较次数
𝐶n =1,𝐶n−1 =2,…,𝐶1 =n,于是,查找成功的时间复杂度为o(n)。 这就是说,查找成功的平均比较次数约为表长的一半。若k值不在表中,则必须进行n+1次比较
之后才能确定查找失败。另处,从ASL可知,当n较大
时,ASL值较大,查找的效率较低。
3、性能分析
在查找成功时的ASL为:
\(ASL_{succ}= \begin{matrix} n \\ Σ \\ i=1 \end{matrix} p_i\times c_i= \begin{matrix} n \\ Σ \\ i=1 \end{matrix} \frac{1}{n}\times i= \frac{1}{n} \begin{matrix} n \\ Σ \\ i=1 \end{matrix} i=\frac{n+1}{2}\)
顺序查找的优点是算法简单,对表结构无任何要求,无论是用向量还是用链表来存放结点,也无论结点之间是否按关键字有序或无序,它都同样适用。顺序查找的缺点是查找效率低,ASL达到了 ,所以时间复杂度为O(n)。
当n较大时,不宜采用顺序查找,而必须寻求更好的查找方法。
折半查找的前提条件是:查找表有序。而是顺序存储结构
1、思想:
折半查找(Binary Search)是用待查找元素的key与查找表的“中间位置”的元素的关键字进行比较,若它们的值相等,则查找成功。若查找元素key大于查找表的“中间位置”的元素的关键字的值,则在查找表的中间位置的后端范围内,继续使用折半查找。否则,则在查找表的中间位置的前端范围内,继续使用折半查找。直到查找成功或者失败为止。
二分查找的具体操作是:首先将待查值K与有序表R[1]到R[n]的中点mid上的关键字R[mid].key进行比较,若相等,则查找成功;否则,若R[mid].key>k , 则在R[1]到R[mid-1]中继续查找,若有R[mid].key<k ,则在R[mid 1]到R[n]中继续查找。每通过 次关键字的比较,区间的长度就缩小一半,区间的个数就增加一倍,如此不断进行下去,直到找到关键字为K的元素;若当前的查找区间为空(表示查找失败)。
从上述查找思想可知,每进行一次关键字比较,区间数目增加一倍,故称为二分(区间一分为二),而区间长度缩小一半,故也称为折半(查找的范围缩小一半)。
|
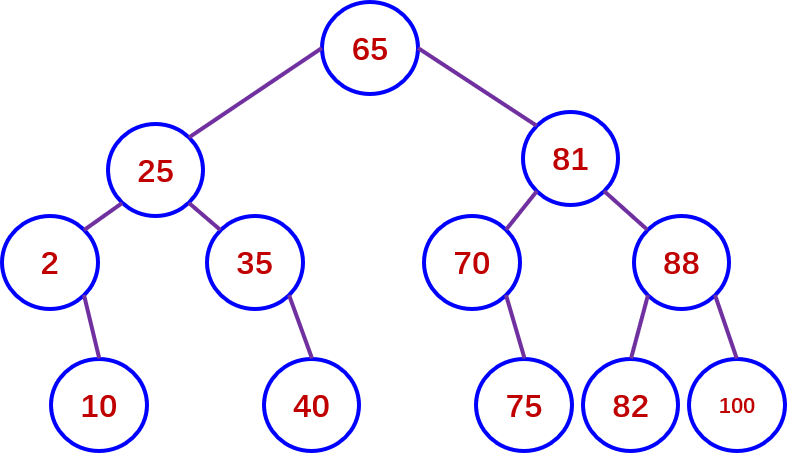
74.计算机组成原理王道最后8套题第二套第一,9题009页 9,折半查找有序表(2,10,25,35,40,65,70,75,81,82,88,100) ,若查找元素75,需依次与表中元素( ) 进行比较。 |
| A.65,82,75 |
| B.70,82,75 |
| C.65,81,75 |
| D.65,81,70,75 |
| D |
|
9. D。 [解析1考查折半查找的查找过程。有序表长12,依据折半查找的思想,第一次查找第⌊(1+12)/2⌋=6个元素,即65;第二次查找第⌊[(6+1)+12]/2⌋=9个元素,即81;由于75在左边所以第三次查找第⌊[7+(9-1)]/2⌋=7个元素,即70;第四次查找第⌊[(7+1)+8]/2⌋=8 个元素,即75。比较的元素依次为65,81,70,75。对应的折半查找判定树如下图所示。
|
10)为确定数据元素在列表中的位置,需和给定值进行比较的关键字个数的期望值,称为查找算法在查找成功时的____
平均查找长度
int binsearch(snode &l,elemtype k)
{ int low,high,mid;
low=1;high=l.len;
while(low<=high)
{ mid=(low+high)/2;//取区间中点
if(l.R[mid].key==k) return mid; //查找成功
else if(l.R[mid].key>k) high=mid-1;//在左子区间中查找
else low=mid+1;}//在右子区间中查找
return 0;
} //查找失败
|
74.计算机组成原理王道最后8套题第四套第一,8题025页 8.在关键字随机分布的情况下,用二分查找树的方法进行查找,其平均查找长度与()量级相当。 |
| A.顺序查找 |
| B. 折半查找 |
| C. 分块查找 |
| D.散列查找 |
| B |
|
8. B. [解析]考查各种查找方法的特点。顾序查找平均查找长度的数量级是0(n); 折半查找平均查找长度的数量级是o(log2n)。分块查找平均查找长度的数量级是O(logzK+n!K)。 散列查找的平均查找长度跟装填因子和采用的冲突解决方法有关。一分 查找树在最坏情况下的平均查找长度为O(n),但在关键字随机分命的情况下,用二分查找树的方法进行查找的平均查找长度的数量级为O(log2n) |
为了分析二分查找的性能,可以用二叉树来描述二分查找过程。把当前查找区间的中点作为根结点,左子区间和右子区间分别作为根的左子树和右子树,左子区间和右子区间再按类似的方法,由此得到的二叉树称为二分查找的判定树。例如,图7-1给定的关键字序列8,17,25,44,68,77,98,100,115,125,的判定树见图7-3。
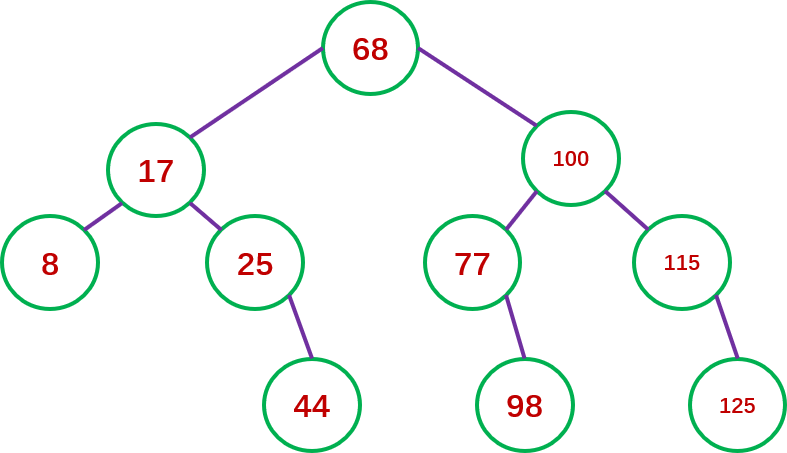
图7-3具有10个关键字序列的二分查找判定树
从图7-3 可知,查找根结点68,需一次查找,查找17和100,各需二次查找,查找8、25、77、115各需三次查找,查找44、98、125各需四次查找。于是,可以得到结论:二叉树第K层结点的查找次数各为k次(根结点为第1层),而第k层结点数最多为2k-1个。假设该二叉树的深度为h, 则二分查找的成功的平均查找长度为(假设每个结点的查找概率相等):
\(ASL=\sum_{i=1}^{n}p_i c_i=\frac{1}{n}\sum_{i=1}^{n}\le\frac{1}{n}(1+2\times2+3\times2^2+...+h\times2^{h-1})\)
因此,在最坏情形下,上面的不等号将会成立 ,并根据二叉树
的性质,最大的结点数n=2h -1,h=log2 (n+1) ,于是可以得到
平均查找长度ASL=(n+1)/nlog2 (n+1)-1。该公式可以按如下
方法推出:
\(s=\sum_{i=1}^{n}k2^{k-1}==2^0+2\times2^1+3\times2^2+\cdots+(h-1)\times2^{h-2}+h\times2^{h-1}\)
则
\(2s=2^1+2\times2^2+\cdots+(h-2)×2^{h-2}+h-1)×2{h-1}+h\times2^h\)
s=2s-2
\(=h\times2^h-(2^0+2^1+2^2+\cdots+2^{h-2}+2{h-1}) \)
\(=h\times2^h-(2^h-1)\)
\(=log_2(n+1)\times(n+1)-n\)
当n很大时,ASL≈ log2 (n+1)-1 可以作为二分查找成功时的平均查找长度,它的时间复杂度为O(log2 n)。
3、性能分析:
我们借助于一棵完全二叉树来分析。
\(ASL_{succ}=\sum_{i=1}^{n}p_i\times c_i\)
2 动态查找
在查找表中实施查找时,对于给定值key,若表中存在关键字值等于key的记录,则查找成功。否则,将待查找记录按规则插入查找表中。
下面我们介绍几种动态查找方法。
:前提是将查找表组织成为一棵二叉排序树。
二叉排序树(Binary Sorting Tree),它或者是一棵空树,或者是一棵具有如下特征的非空二叉树:
(1)若它的左子树非空,则左子树上所有结点的关键字均小于根结点的关键字;
(2)若它的右子树非空,则右子树上所有结点的关键字均大于等于根结点的关键字;
(3)左、右子树本身又都是一棵二叉排序树。
例如,结定关键字序列79,62,68,90,88,89,17,5,100,120,生成二叉排序树过程如图7-6所示。(注:二叉排序树与关键字排列顺序有关,排列顺序不一样,得到的二叉排序树也不一样)
|
74.数据结构王道最后8套题第六套第一,4题041页 4.含有4个元素值均不相同的结点的二叉排序树有()种 。 |
| A.4 |
| B.6 |
| C.10 |
| D. 14 |
| D |
|
4. D。【解析】考查二叉排序树。分别设4 个元素值为 1、2、3、4,构造二叉排序树:在 1 为根时,对应 2、3、4 为右子树结点,右子树可有 5 种对应的二 叉排序树;在 2 为根时,对应 1 为左子树,3、4 为右子树结点,可有 2 种二叉排序树;在 3 为根时,1、2 为左子树结点,4 为右子树,可有 2 种二叉排 序树;在4 为根时,1、2、3 为左子树结点,对应二叉排序树有 5 种。因此共有 5+2+2+5=14 种。 |
3.查找效率
查找效率平均查找长度(ASL)取决于树的高度。
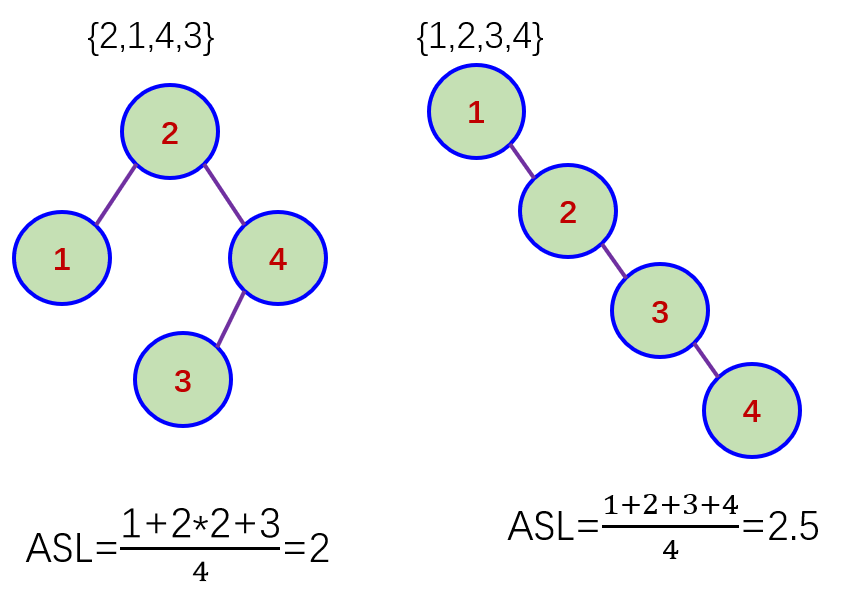
为平衡二叉树时候效率高
4.二叉排序 树上的查找
(1)二叉排序 树的查找思想
若二叉排树为空,则查找 失败,否则,先拿根结点值与待查值进行比较,若相等,则查找成功,若根结点值大于待查值,则进入左子树重复此步骤,否则,进入右子树重复此步骤,若在查找过程中遇到二叉排序树的叶子结点时,还没有找到待找结点,则查找不成功。
(2)二叉排序树查找的算法实现
bitree * find( bitree *bst,elemtype x)
//在以bst为根指针的二叉排队 树中查找值为x的结点
{ if ( bst= =NULL)
return NULL; //查找失败
else {
if (bst->data= =x) //查找成功
return bst;
else if (bst->data>x) //进入左子树查找
return find ( bst->lchild,x);
else return find (bst->rchild,x);} //进入右子树查找
}
74.数据结构王道最后8套题第五套第二,41题038页
41. (12分)设记录的关键字(key)集合: K={24,15,39,26,18,31,05,22},请回答:
(1)依次取K中各值,构造一棵二叉排序树(不要求平衡),并写出该树的前序、中序和后序遍历序列。
(2)设Hash表表长m=16,Hash 函数H(key)=(key)%13,处理冲突方法为“二次探测法”,请依次取K中各值,构造出满足所给条件的Hash表;并求出等概率条件下查找成功时的平均查找长度。
(3)将给定的K调整成一个堆顶元素取最大值的堆(即大根堆)。
(1)将关键字{24, 15,39, 26,18, 31,05, 22}依次插入构成的二义排序树如下:
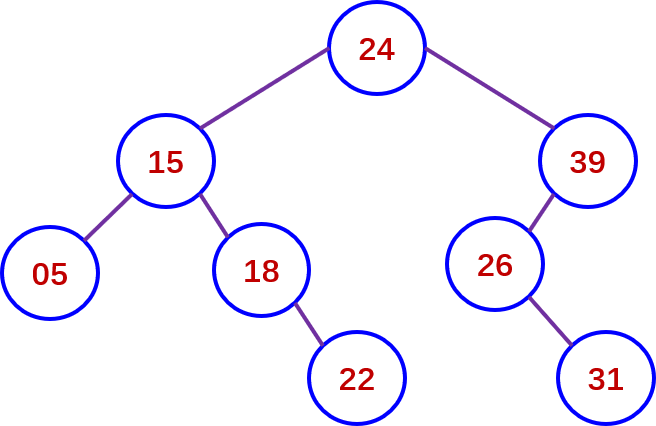
先序遍历序列: 24, 15,05,18, 22,39,26,31
中序遍历序列: 05,15,18, 22,24,26,31,39
后序遍历序列: 05, 22, 18, 15, 31,26,39,24
(2)各关键字通过Hash函数得到的散列地址如下表。
|
关键字 |
24 |
15 |
39 |
26 |
18 |
31 |
05 |
22 |
|
散列地址 |
11 |
2 |
0 |
0 |
5 |
5 |
5 |
9 |
Key=24、15、39均没有冲突,
H0(26)=0, 冲突,𝐻1H_1(26)=0+1=1, 没有冲突;
Key=18 没有冲突,
H0(31)=5,冲突,H1(31)=5+1=6,没有冲突;
H0(05)=5,冲突,H1(05)=5+1= 6,冲突,H2(05)=5-1=4,没有冲突;
Key=22 没有冲突.
故各个关键字的存储地址如下表所示。
|
地址 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
关键字 |
39 |
26 |
15 |
|
05 |
18 |
31 |
|
|
22 |
|
24 |
|
|
|
没有发生冲突的关键字,查找的比较次数为1, 发生冲突的关键字,查找的比较次数为冲突次数+1,因此,等概率下的平均查找长度为:
ASL=(1+1+1+2+1+2+3+1)/8=1.5次
(3)首先对以26为根的子树进行调整,调整后的结果如图b所示:对以39为根的子树进行调整,调整后的结果如图c所示;再对以15为根的子树进行调整,调整后的结果如图d所示;对根结点进行调整,调整后的结果如图e所示。
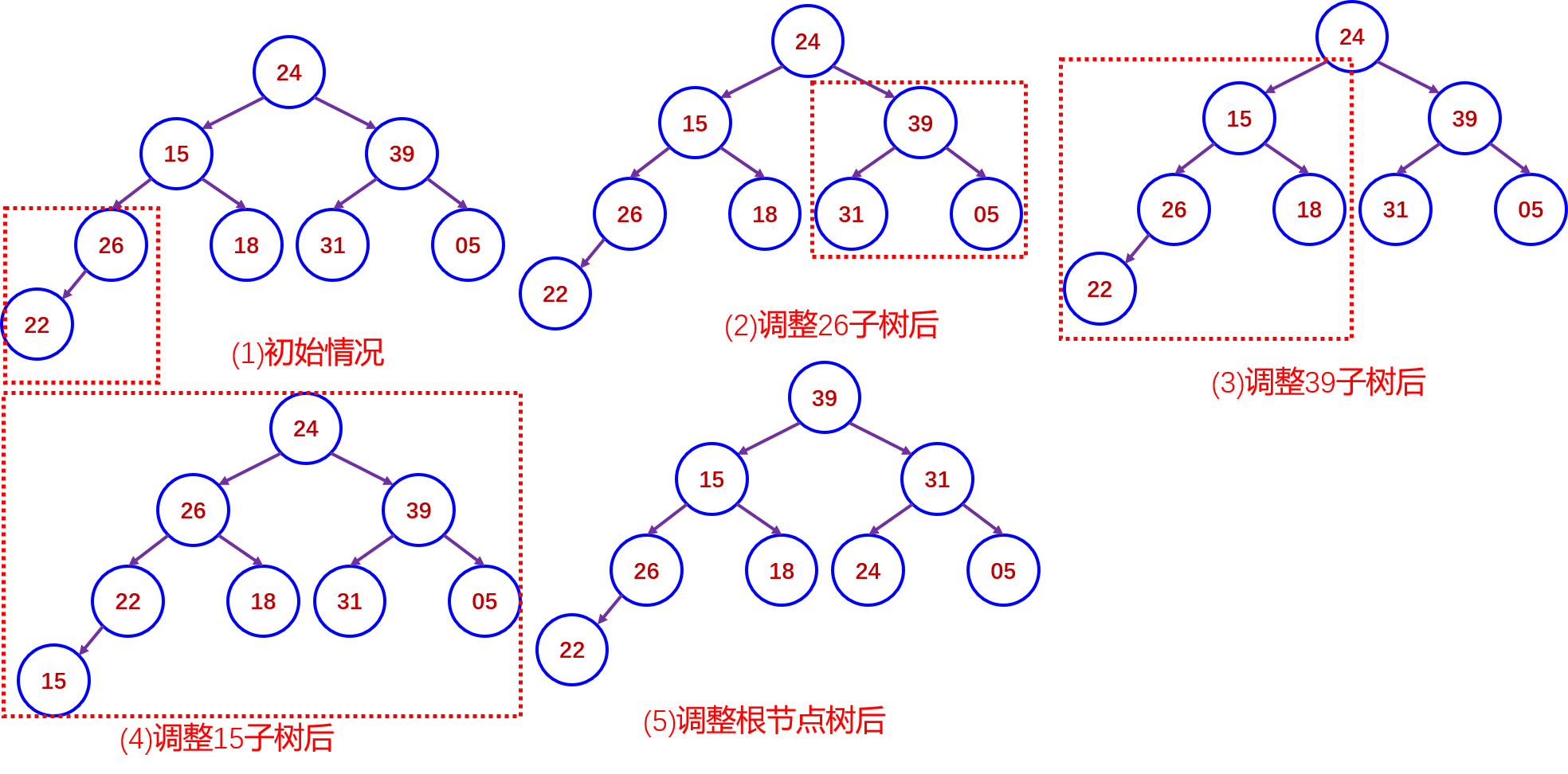
|
数据结构王道最后8套题第五套第一,6题033页 6.以下关于二叉排序树的说法中,错误的有( ) 个。 I.对一棵二叉排序树按前序遍历得出的结点序列是从小到大的序列 II.每个结点的值都比它左孩子的值大、比它右孩子结点的值小,则这样的一棵二叉权就是二叉排序树 llI.在二叉排序树中,新插入的关键字总是处于最底层 IV.删除二义排序树中的一一个结点再重新插入,得到的二叉排序树和原来的相同 |
| A. 1 |
| B.2 |
| C.3 |
| D.4 |
| D |
|
6. D。 [解析]考查一叉排序树的性质。二叉排序树的中序序列才是从小到大有序的,I 错误。左子树上所有的值均小于根结点的值:右子树上所有的值均大于根结点的值,而不仅仅是与左、右孩子的值进行比较,II 错误(举例如右图),
应改为比左子树上的所有结点都小,比右子树上的所有结点都大。新插入的关键字总是作为叶结点来插入,但叶结点不一定总是处于最底层,II错误。当删除的是非叶结点时,根据II的解释, 显然重新得到 75的二叉排序树和原来的不同:只有当删除的是叶结点时,才能得到和原来一样的二叉排序树,IV错误。 |
5.二叉排序树查找的性能分析
在二叉排序树查找中,成功的查找次数不会超过二叉树的深度,而具有n个结点的二叉排序树的深度,最多为log2n,最坏为n。
因此,二叉排序树查找的最好时间复杂度为O(log2n),最坏的时间复杂度为O(n),一般情形下,其时间复杂度大致可看成O(log2n),比顺序查找效率要好,但比二分查找要差。
6.二叉排序树删除
在二叉排序树中删除一一个结 点时,必须确保删除结点后的二叉排序树仍满足二叉排序树的定义。删除操作的实现过程按以下三种情况来处理:
①如果被删除结点x是叶结点,则直接删除。
②若结点x只有一棵左子树或右子树,则让x的子树成为x父结点的子树,替代x的位置。
③若结点x有左、右两棵子树,则令x的中序后继(或前驱)替代x,然后从二叉排序树中
删去这个直接后继(或直接前驱),这样就转换成了第一-或第二种情况。。
如图4-4所示,在后两种情况下分别删除结点的过程。。
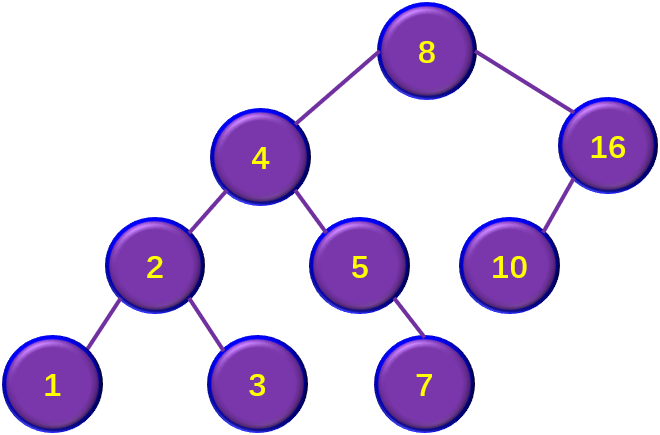
1)若被删除结点z是叶结点,则直接删除;
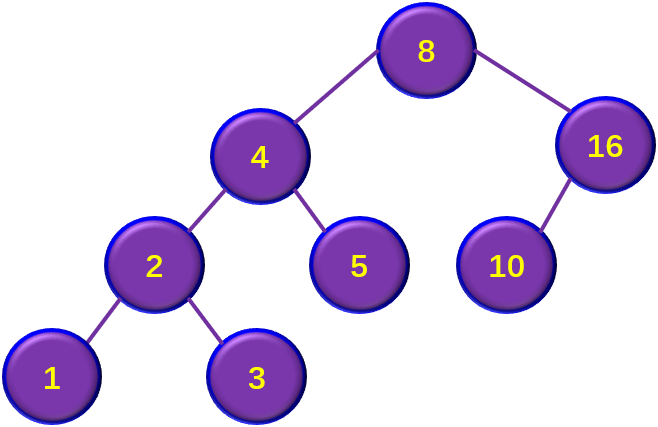
2)若被删除结点z只有一棵子树,则让z的子树成为z父结点的子树,代替z结点。
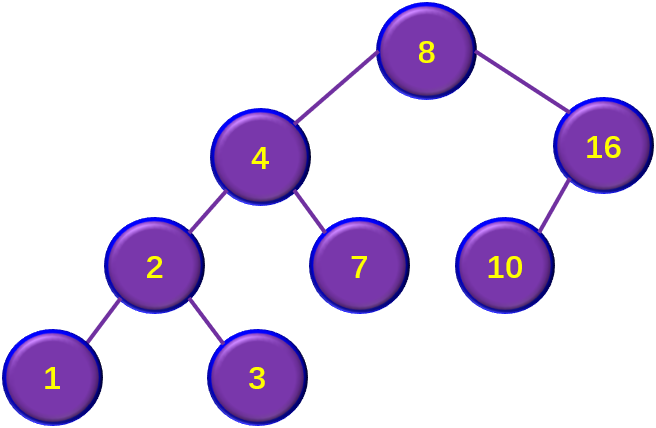
3)若被删除结点z有两棵子树,则让z的中序序列直接后继代替z,并删去直接后继结点。
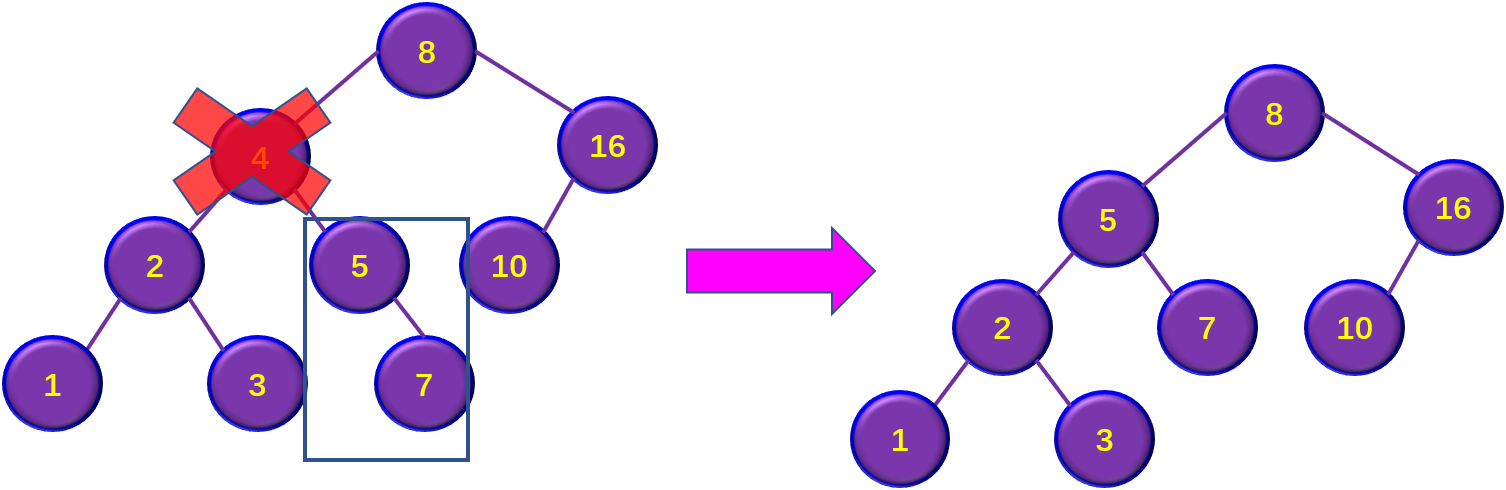
4)在二叉排序树中删除并插入某节点,得到的二叉排序树是否与原来相同
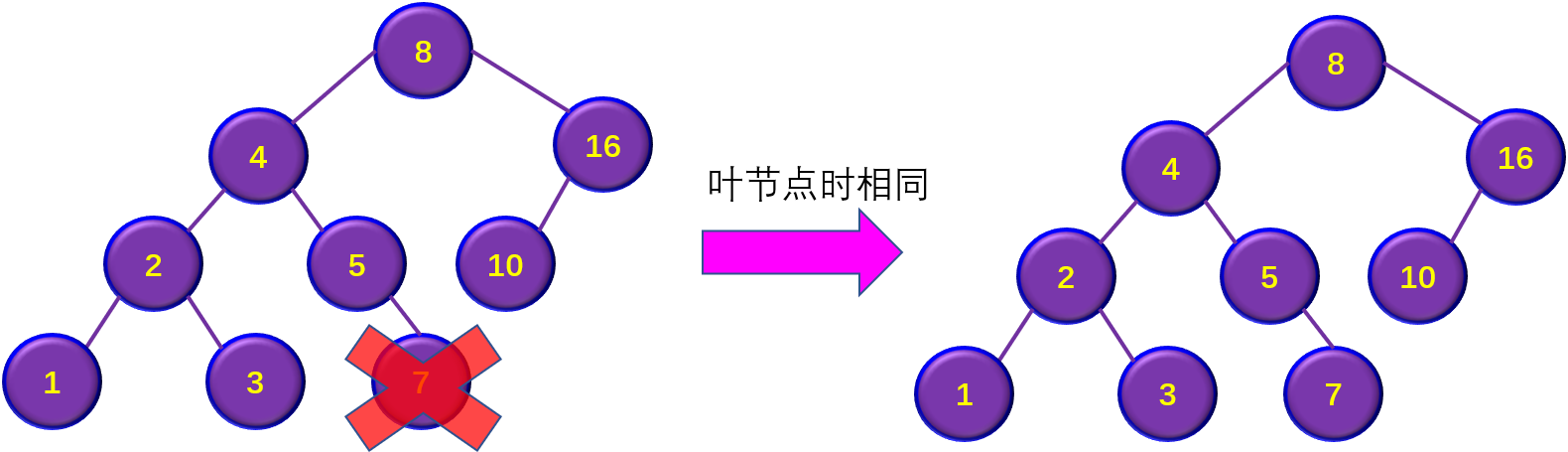
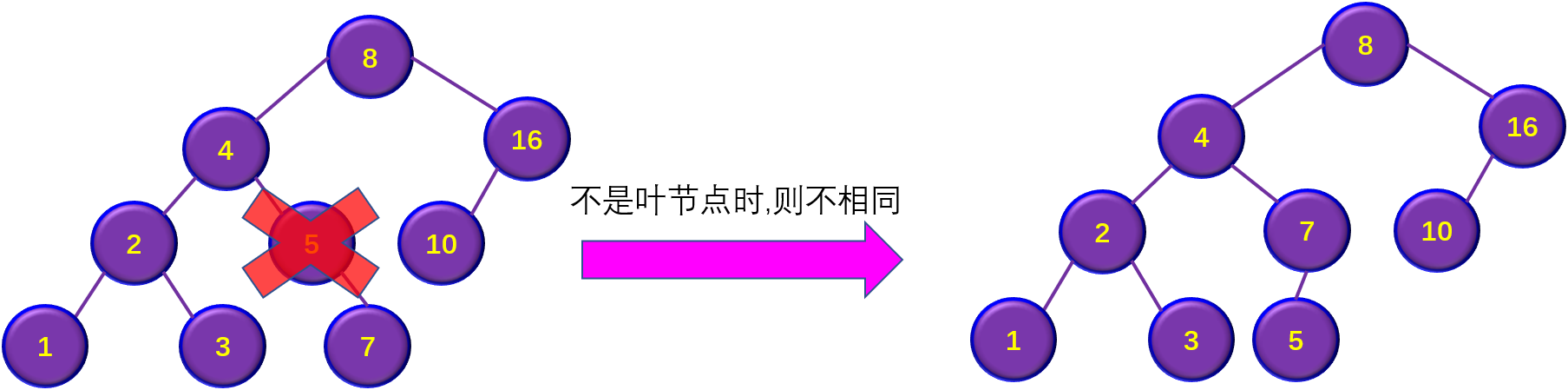
二叉排序树→调整→平衡二叉树
平衡二叉树(balanced binary tree)是由阿德尔森一维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树。
若一棵二叉树中每个结点的左、右子树的深度之差的绝对值不超过1,则称这样的二叉树为平衡二叉树。将该结点的左子树深度减去右子树深度的值,称为该结点的平衡因子(balance factor)。也就是说,一棵二叉排序树中,所有结点的平衡因子只能为0、1、-1时,则该二叉排序树就是一棵平衡二叉树,否则就不是一棵平衡二叉树。如图7-8所示二叉排序树,是一棵平衡二叉树,而如图7-9所示二叉 排序树,就不是一棵平衡二叉树 。
|
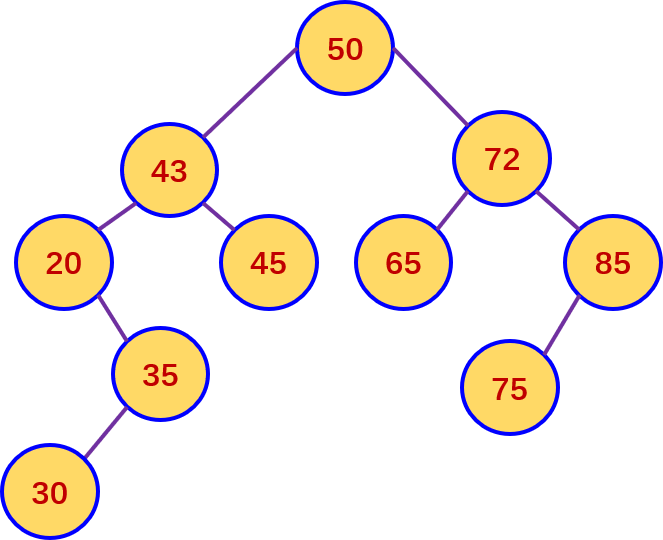
74.数据结构王道最后8套题第六套第一,5题041页 5.由元素序列(27,16,75,38,51) 构造平衡二叉树,则首次出现的最小不平衡子树的根(即离插入结点最近且平衡因子的绝对值为2的结点)是( )。 |
| A.27 |
| B. 38 |
| C.51 |
| D.75 |
| D |
|
5.D。 【解析】考查平衡二叉树的构造。由题中所给的结点序列构造平衡二叉树的过程如图 1 所示,当插入 51 后,首次出现不平衡子树,虚线框内即为最小不平衡子树。
|
|
74.数据结构王道最后8套题第三套第一,5题017页 5.按含有20个结点的平衡二叉树的最大深度为() |
| A.4 |
| B.5 |
| C.6 |
| D.7 |
| C |
|
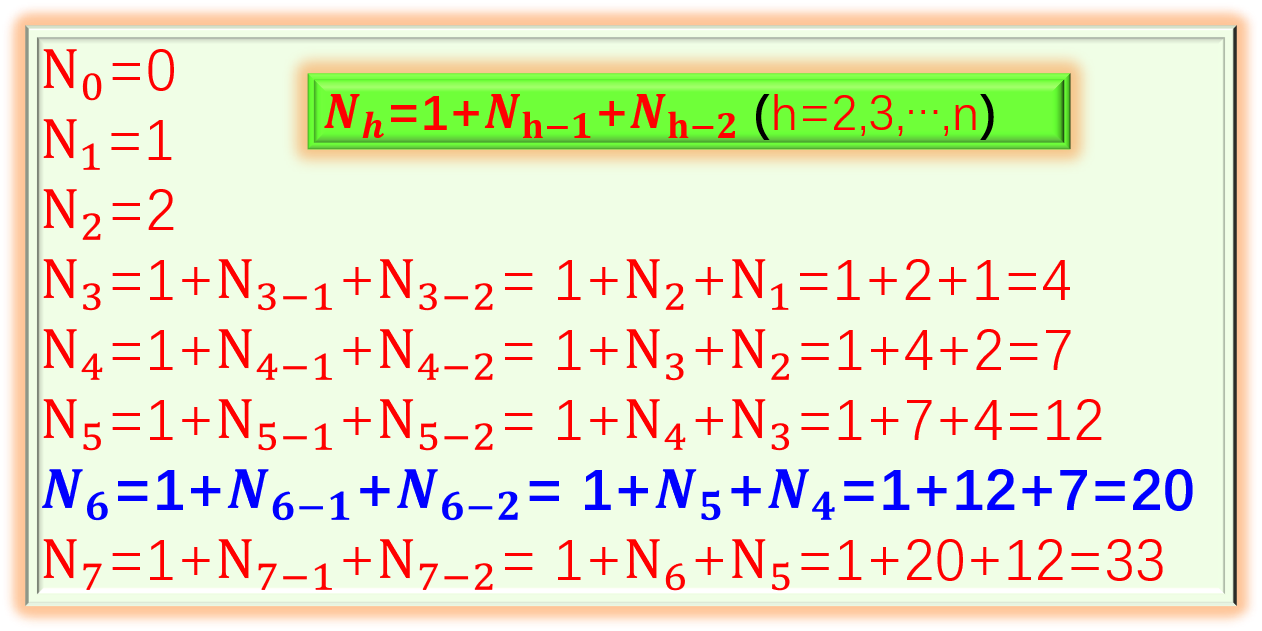
5. C。 [解析]考查平衡二叉树的性质。在平衡二叉树的结点最少情况下,递推公式为N0=0,N1=1,N2=2,Nh=1+Nh−1+Nh−2 (h为平衡二叉树高度,Nh为构造此高度的平衡二叉树所需最少结点数)。通过递推公式可得,构造5层平衡二叉树至少需12个结点,构造6层至少需要20个。
|
(边创建边调整)
若一棵二叉排序树是平衡二叉树,插入某个结点后,可能会变成非平衡二叉树,这时,就可以对该二叉树进行平衡处理,使其变成一棵平衡二叉树。处理的原则应该是处理与扦入点最近的、而平衡因子又比1大或比-1小的结点。下面将分四种情况讨论平衡处理。
|
74.数据结构王道最后8套题第八套第一,6题057页 6.在含有 15 个结点的平衡二叉树上,查找关键字为 28(存在该结点)的结点,则依次比较的关键字有可能是( )。 |
| A.30,36 |
| B.38,48,28 |
| C.48,18,38,28 |
| D.60,20,50,40,38,28 |
| C |
|
6.C。 【解析】考查平衡二叉树的性质与查找操作。设 Nh表示深度为h 的平衡二叉树中含有的最少结点数,有: N0=0,N1=1,N2=2,…,Nh=Nh-1+Nh-2+1,N3=4, N4=7,N5=12,N6=20>15(考生应能画出图形)。也就是说,高度为 6 的平衡二叉树最少有 20 个结点,因此 15 个结点的平衡二叉树的高度为 5,而最小叶子结点的层数为 3,所以选项D 错误。选项B 的查找过程不能构成二叉排序树,错误。选项A 根本就不包含 28 这个值,错误。 |
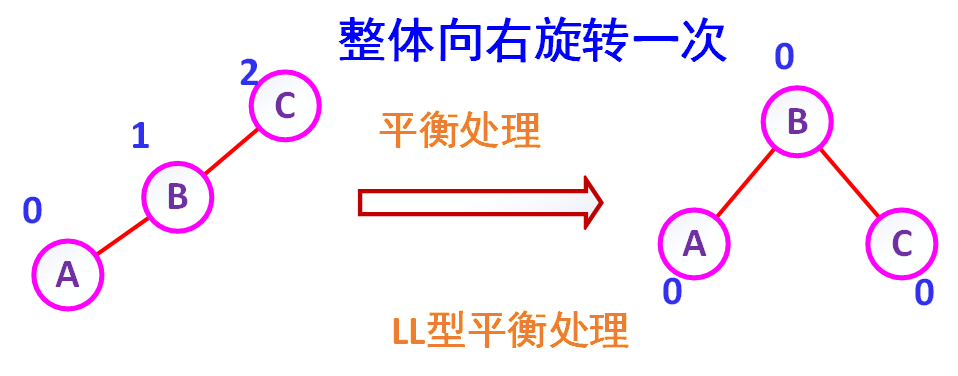
(1)LL型 的处理(左左型)
如图7-10所示,在C的左孩子B上扦入一个左孩子结点A,使C的平衡因子由1变成了2,成为不平衡的二叉树序树。这时的平衡处理为:将C顺时针旋转,成为B的右子树,而原来B的右子树则变成C的左子树,待扦入结点A作为B的左子树。(注:图中结点旁边的数字表示该 结点的平衡因子)
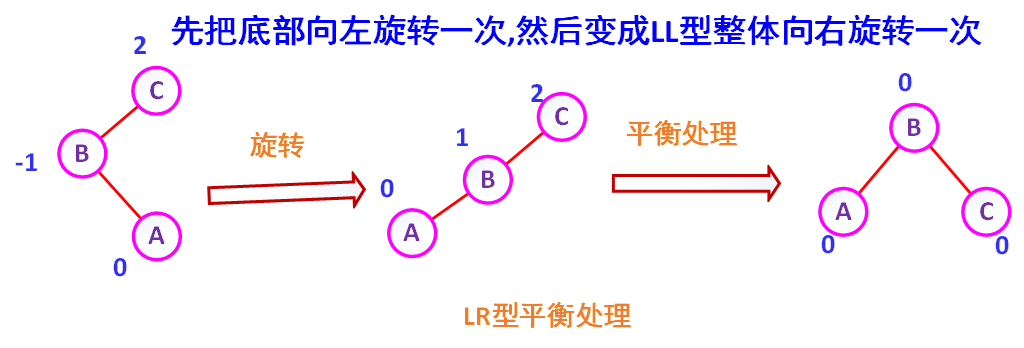
(2)LR型的处理(左右型)
如图7-11所示,在C的左孩子A上扦入一个右孩子B,使的C的平衡因子由1变成了2,成为不平衡的二叉排序树。这是的平衡处理为:将B变到A与C 之间,使之成为LL
( 型,然后按第(1)种情形LL型处理。
(3)RR型的处理(右右型)
如图7-12所示,在A的右孩子B上扦入一个右孩子C,使A的平衡因子由-1变成-2,成为不平衡的二叉排序树。这时的平衡处理为:将A逆时针旋转,成为B的左子树,来 点 而原来B的左子树则变成A的右子树,待扦入结点C成为B的右子树。
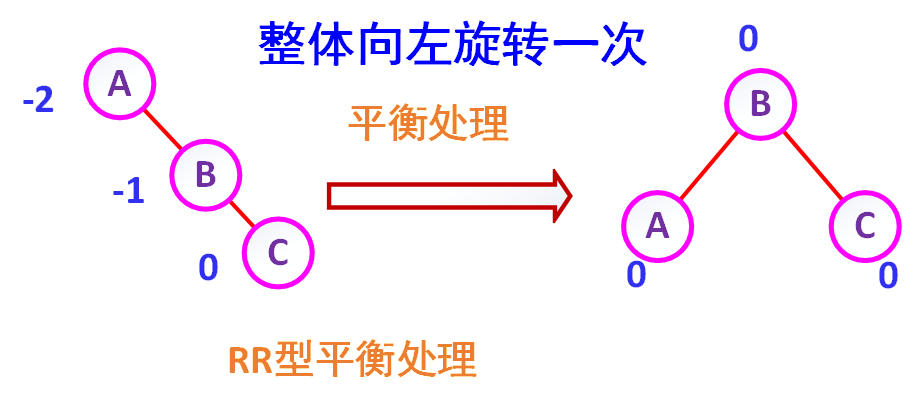
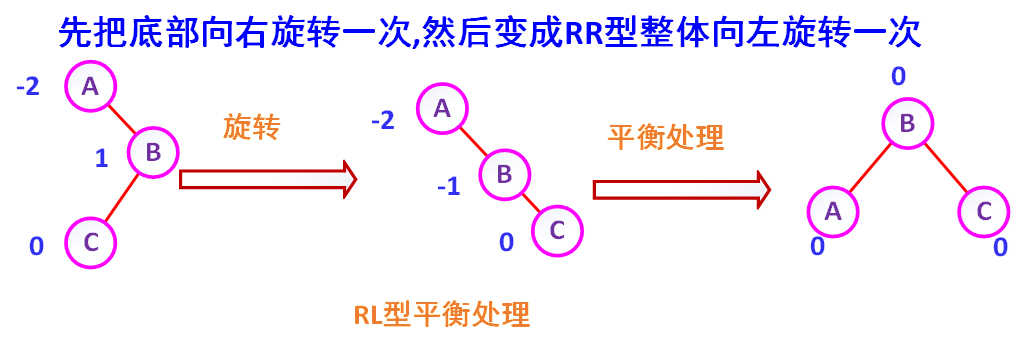
(4)RL型的处理(右左型)
如 图7-13所示,在A的右孩子C上扦入一个左孩子B,使A的平衡因子由-1变成-2,成为不平衡的二叉排序树。这时的平衡处理为:将B变到A与C之间,使之成为RR型,( 然后按第(3) 种情形RR型处理。
平衡树的查找性能分析:
在平衡树上进行查找的过程和二叉排序树相同,因此,查找过程中和给定值进行比较的关键字的个数不超过平衡树的深度。
因此,在平衡二叉树上进行查找时,查找过程中和给定值进行比较的关键字的个数和相当。
|
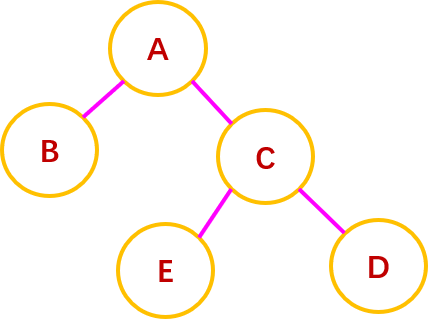
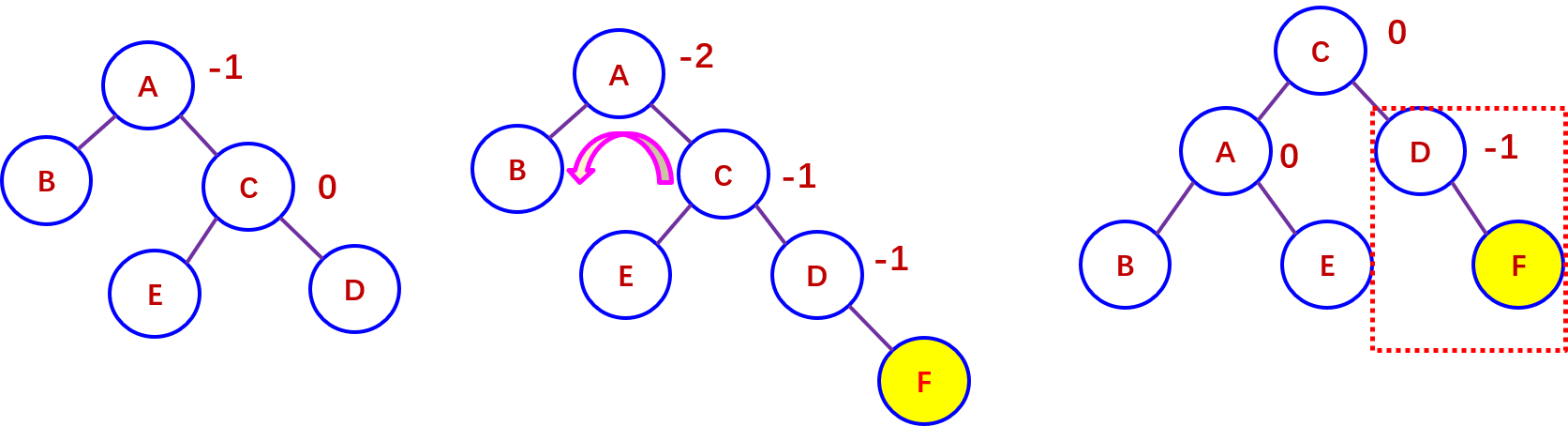
74.数据结构王道最后8套题第七套第一,5题050页 5.如图所示为一棵平衡二叉树(字母不是关键字),在结点D 的右子树上插入结点F 后,会导致该平衡二叉树失去平衡,则调整后的平衡二叉树中平衡因子的绝对值为 1 的分支结点数为( )。 |
| A.0 |
| B.1 |
| C.2 |
| D.3 |
| B |
|
5.B。 【解析】考查平衡二叉树的旋转。由于在结点 A 的右孩子(R)的右子树(R)上插入新结点 F,A 的平衡因子由−1 减至−2,导致以 A 为根的子树失去平衡,需要进行 RR 旋转(左单旋)。 RR 旋转的过程如上图所示,将 A 的右孩子 C 向左上旋转代替 A 成为根结点,将 A 结点向左下旋转成为 C 的左子树的根结点,而 C 的原来的左子树 E 则作为A 的右子树。故,调整后的平衡二叉树中平衡因子的绝对值为 1 的分支结点数为1。 注意:平衡旋转的操作都是在插入操作后,引起不平衡的最小不平衡子树上进行的,只要将这个最小不平衡子树调整平衡,则其上级结点也将恢复平衡。
|
介绍一种不通过大量无效的比较,就能直接找到待
查关键字的位置的查 找方法
一、基本术语
1、Hash方法:
在存放记录时,通过相同函数计算存储位置,并按此位置存放,这种方法称为Hash方法。
2、Hash函数:是指在Hash方法中使用的函数。
3、Hash表:
按Hash方法构造出来的表称为Hash表。
4、Hash地址:
通过Hash函数计算记录的存储位置,我们把这个存储位置称为Hash地址。
5、冲突(Collision):
不同记录的关键字经过Hash函数的计算可能得到同一Hash地址,即key 1 ≠key 2 时,H(key 1 )=H(key 2 )。这种现象叫做“冲突” 。
对于Hash方法需要讨论三个问题:
(1)装满因子
(2)对于给定的一个关键码集合,选择一个计算简单且地址分布比较均匀的Hash函数,避免或尽量减少冲突。
(3)拟订解决冲突的方案。
装满因子
在哈希存贮中,若发生冲突,则必须采取特殊的方法来解决冲突问题,才能使哈希查找能顺利进行。虽然冲突不可避免,但发生冲突的可能性却与三个方面因素有关。第一是与装填因子α有关,所谓装填因子是指哈希表中己存入的元素个数n与哈希表的大小m的比值,即α=n/m。当α越小时,发生冲突的可能性越小,α越大(最大为1)时,发生冲突的可能性就越大。但是,为了减少冲突的发生,不能将α变得太小,这样将会造成大量存贮空间的浪费,因此必须兼顾存储空间和冲突两个方面。第二是与所构造的哈希函数有关(前面己介绍)。第三是与解决冲突的方法有关,这些内容后面将再作进一步介绍。
⑴、计算Hash函数所需的时间;
⑵、关键字的长度;
⑶、Hash表的大小;
⑷、关键字的分布情况;
⑸、记录的查找频率。
⑴.直接定址法
此类方法取记录中关键码的某个线形函数值作为
Hash地址:
Hash(key)=a*key+b
其中:a,b为常数
这类Hash函数是一对一的映射,一般不会产生冲突。但是,它要求Hash地址空间的大小与关键码集合的大小相同,这种要求一般很难实现。
⑵.数字分析法
设有n个d位数,每一位可能有r种不同的符号。这r种不同的符号在各位上出现的频率不一定相同。可根据Hash表的大小,选取其中各种符号分布均匀的若干位作为Hash地址。
计算各位数字中符号分布均匀度的公式:
\(λ_i=\sum_{i=1}^{r}(a_{i}^{k}-\frac{n}{r})^2\)
其中,\(a_{i}^{k}\) 表示第i个符号在第k位上出现的次数,\(\frac{n}{r}\)表示各种符号在n个数中均匀出现的期望值。计算λi 的值越小,表明在该位各种符号分布的越均匀。
⑶除留余数法
设Hash表中允许的地址数为m,取一个不大于m,但最接近或等于m的质数p,或选取一个不含有小于20的质因子的合数作为除数。这样的Hash函数为:
Hash(key) = key % p (p≤m)
其中:“%”是整数除法取余的运算,要求这时的质数p不是接近2的幂。
这是一种常用的构造Hash函数的方法。
一散列表长度m为100,采用除留余数法构造散列函数,即H(K)=K%P (P<=m),,为使散列函数具有较好的性能,P的选择应是()
97 取一个不大于,但最接近的质数
⑷平方取中法
先计算构成关键码的表示符的内码的平方,然后按照Hash表的大小取中间的若干位作为Hash地址。在平方取中法中,一般取Hash地址为2的某次幂。
⑸折叠法
有两种方法:
(1)、移位法是把各部分的最后一位对齐相加。
(2)、分界法是把各部分不折断,沿各部分的分界来回折叠,然后对齐相加,将相加的结果当作散列地址。
下面是折叠法的示例:
例如,假设关键字为某人身份证号码430104681015355,则可以用4位为一组进行叠加,即有5355+8101+1046+430=14932,舍去高位,则有H(430104681015355)=4932为该身份证关键字的哈希函数地址。
⑹.随机数法
所谓随机数法(random)是指为Hash表中的关键字
选取一个随机函数值作为其Hash地址。即:H(key)=random(key)
其中:random为随机函数
通常在Hash表中的关键字长度不等时,采用此方法
构造Hash函数比较合适。
所谓开放地址法是指在冲突发生时,产生某个探测序列,按照这个序列,探测在Hash表中的其它存储单元,直到探测到不发生冲突的存储单元为止。我们可以用下述公式来描述: H i (key)=(H(key)+d i )% m (i=1,2,…,m)
其中:H i (key)为经过i次探测H(key)为关键字key的直接Hash地址,m为Hash表的长度,d i 为每次再探测时的地址增量。 这种方法容易产生“淤积(full-up)”现象。
一般情况下,地址增量的取值有以下三种:
1、d i =1,2,…,m-1 称这种情况为线性探测再Hash;
2、d i =1 2 ,-1 2 ,2 2 ,-2 2 ,3 2 ,…,±k 2 (k≤m/2) 称这种情况为二次探测再Hash;
3、d i =伪随机函数 称这种情况为伪随机探测再Hash;
例:设Hash函数为:H(key)=key % 7,Hash表的地址范围为0到6,对关键字序列(25,6,42,11,15,31,14)按线性探测再Hash和二次探测再Hash解决冲突构造Hash表。
链地址法处理冲突的方法是,将通过Hash函数计算出来的Hash地址相同的关键码通过链表链接起来,各链表表头结点组成一个向量。向量的元素个数与关键字个数相同。
例:设Hash函数为:H(key)=key % 7,Hash表的地址范围为0到6,对关键字序列(25,6,42,11,15,31,14)按链地址法解决冲突构造的Hash表。
74.数据结构王道最后8套题第三套第二,41题017页
41. (12分)使用散列函数hashf(x)=x mod 11,把一个整数值转换成散列表下标,现要把数据: 1,13,12,34,38,33,27,22插入到散列表中。
(1)使用链地址的冲突处理方法来构造散列表。
(2)分别计算等概率情况下,查找成功和查找不成功所需的平均探查长度。(假设探查到空结点也算一次探查)
(3)若查找关键字34,则需要依次与哪些关键字比较。
41.解析:
(1)采用链地址法构造散列表时,在直接计算出关键字对应的哈希地址后,将关键字结点插入到此哈希地址所在的链表中。 由hashf(x)=x mod 11可知,散列地址空间是0到10。链地址法构造的表如下:
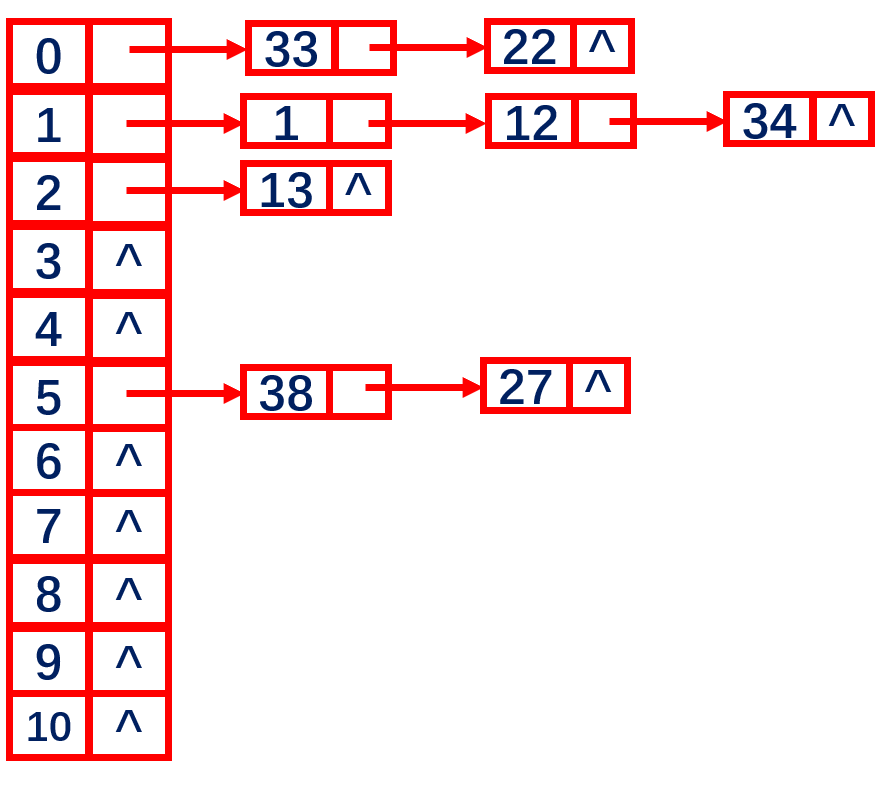
(2)在链地址表中查找成功时,查找关键字为33的记录需进行1次探测,查找关键字为22的记录需进行2次探测,依此类推。因此:
ASL成功=(1x4+2x3+3)/8=13/8
查找失败时,假设对空结点的查找长度为1,则对于地址0,查找失败的探测次数为3;对于地址1,查找失败的探测次数为4,则平均探查长度为:
ASL失败ASL_失败=\(\frac{3+4+2+1+1+3+1+1+1+1+1}{11}\)=\(\frac{19}{11}\)
(3)由(1)可知,查找关键字34,需要依次与关键字1.12.34 进行比较。
[扩展]对同样一组关键字,设定相同的散列函数, 则不同处理冲突方法将得到不同的散列题目应如何解答?
建立公共溢出区是指当冲突发生时,将这些关键字存储在另设立的一个公共溢出区中。具体的做法是:假设Hash地址区间为0到m-1,设向量HashTable[m]为基本表,每一个分量存放一个记录,另外设一个向量OverTable[n]为溢出表。将所有与基本表中关键字冲突的记录,都存放在该溢出表中
例:设Hash函数为:H(key)=key % 7,Hash表的地址
范围为0到6,对关键字序列(25,6,42,11,15,31,
14)按建立公共溢出区解决冲突构造Hash表。
所谓再Hash法是指当冲突发生时,采用另一个Hash函数计算关键字的Hash地址。即构造一系列的Hash函数H 1 (key),H 2 (key),…,H k (key),当冲突发一 生时,依次检查所构造 系列的Hash函数所得到的Hash地址是否为空。这种方法不易产生“淤积”现象,但却增加了计算时间。
1. 给定一组关键字{20,30,50,52,60, 68,70},给出创建一棵3阶B树的过程。
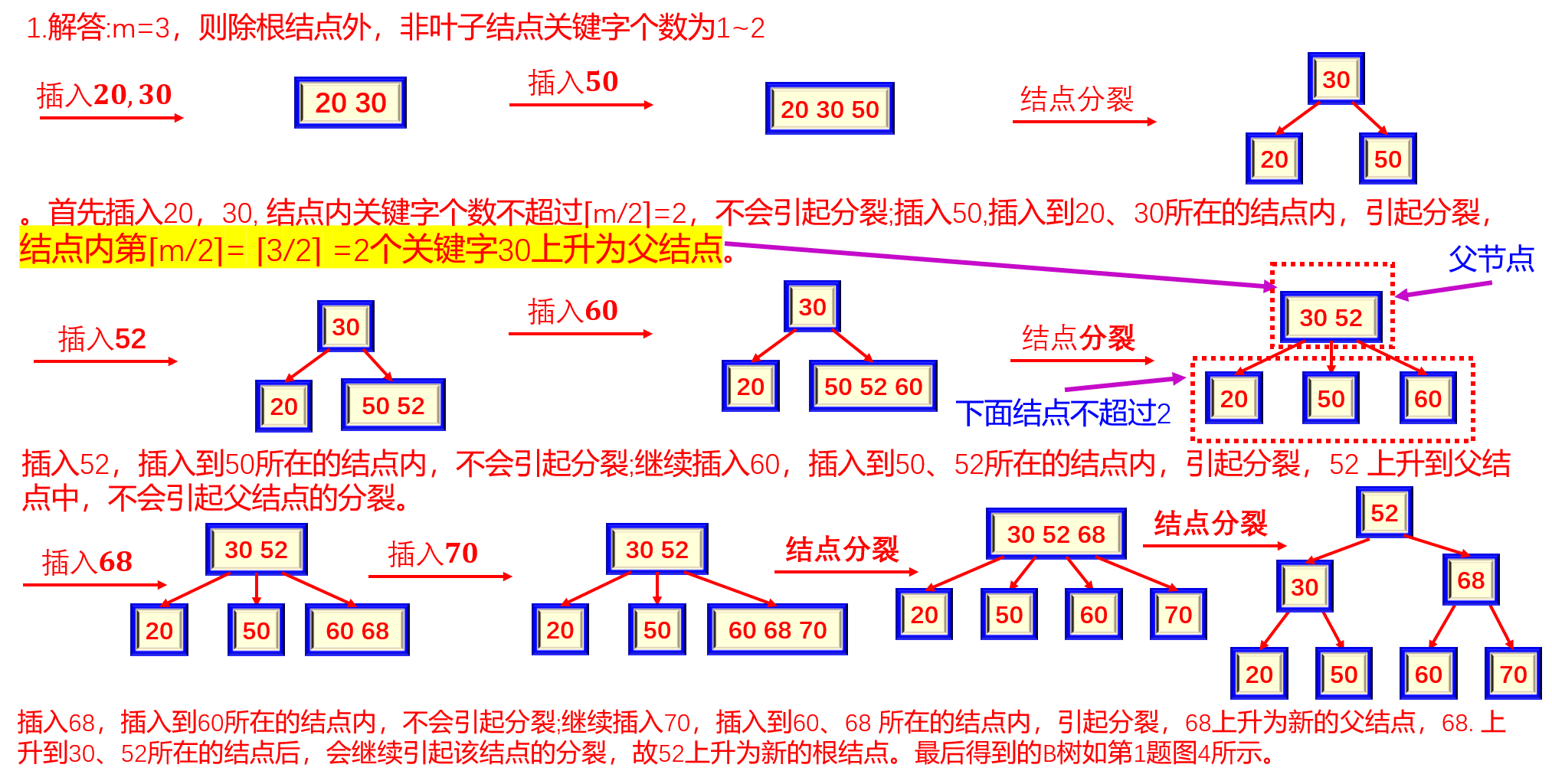
本文作者: 永生
本文链接: https://yys.zone/detail/?id=106
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明出处!

评论列表 (0 条评论)